Tổng hai số tự nhiên a,b thỏa mãn là

Những câu hỏi liên quan
Tổng hai số tự nhiên a, b thỏa mãn:(a+1)^2+(b-2)^2 là
Biết a,b là hai số tự nhiên, nguyên tố cùng nhau và thỏa mãn 3a-2b/ a +5b= 11/ 15. khi đó tổng a+b bằng
tổng hai số tự nhiên a,b thỏa mãn:(a+1)^2+(b-2)^2=4 là
ai giup mk voi dag voi
Tổng hai số tự nhiên a;b thỏa mãn (a+1)2+(b-2)2=4
cho hai số tự nhiên a và b thỏa mãn 12 < a < b 16. Số cặp số a và b thỏa mãn là
Cho hai số tự nhiên a và b thỏa mãn 12 < a < b< 16. Số cặp số a và b thỏa mãn là
khi a là các số 13 , 14
trong khi b = a + 1 , tức là khi a = 13 , thì b = a + 1 = 14 , a = 14 thì b= 14 + 1 = 15
các cặp số a , b cần tìm là (13 , 14) , (14 , 15)
Đúng 0
Bình luận (0)
Tìm hai số tự nhiên a, b với a+2.b=49, đồng thời thỏa mãn điều kiện: Tổng của ước số chung( a, b) và bội số chung( a, b) là 56.
Giúp mik nhá m.n
Bài 4.
1) Cho hai số tự nhiên a và b thỏa mãn số:
m=(16a+17b)(17a+16b) là một bội số của 11. Chứng minh rằng số m cũng là một bội số của 121
2) Tìm tổng tất cả các số tự nhiên có hai chữ số không chia hết cho 3 và 5
Xem chi tiết
Để chứng minh rằng số m cũng là một bội số của 121, ta cần chứng minh rằng (16a+17b)(17a+16b) chia hết cho 11 và 121.
Đầu tiên, chúng ta xét xem (16a+17b)(17a+16b) chia hết cho 11 hay không. Ta biểu diễn số m = (16a+17b)(17a+16b) dưới dạng m = 272a^2 + 528ab + 272b^2.
Vì 11 là một số nguyên tố, nên theo tính chất của phép nhân, để m là một bội số của 11, thì mỗi thành phần của m cũng phải là một bội số của 11.
Ta thấy rằng 272a^2 và 272b^2 đều chia hết cho 11, vì 272 chia hết cho 11. Vì vậy, ta chỉ cần chứng minh rằng 528ab chia hết cho 11 để kết luận m là một bội số của 11.
Để chứng minh điều này, ta sử dụng tính chất căn bậc hai modulo 11. Ta biết rằng căn bậc hai của 11 là 5 hoặc -5 (vì 5^2 = 25 ≡ 3 (mod 11)). Vì vậy, ta có:
(16a+17b)(17a+16b) ≡ (5a+6b)(6a+5b) (mod 11).
Mở ngoặc, ta được:
(5a+6b)(6a+5b) ≡ 30ab + 30ab ≡ 60ab ≡ 6ab (mod 11).
Vì 6 không chia hết cho 11, nên 6ab cũng không chia hết cho 11. Do đó, ta kết luận rằng 528ab không chia hết cho 11 và m là một bội số của 11.
Tiếp theo, chúng ta cần chứng minh rằng m là một bội số của 121. Để làm điều này, ta cần chứng minh rằng m chia hết cho 121.
Một cách để chứng minh rằng m chia hết cho 121 là tìm một số tự nhiên k sao cho m = 121k. Để làm điều này, chúng ta cần tìm một số tự nhiên k sao cho (16a+17b)(17a+16b) = 121k.
Ta biểu diễn số m = (16a+17b)(17a+16b) dưới dạng m = 272a^2 + 528ab + 272b^2.
Chúng ta đã chứng minh rằng m là một bội số của 11, vậy m = 11m' với m' là một số tự nhiên.
Thay thế m vào công thức m = 272a^2 + 528ab + 272b^2, ta có:
11m' = 272a^2 + 528ab + 272b^2.
Chia cả hai vế của phương trình cho 11, ta có:
m' = 24a^2 + 48ab + 24b^2.
Như vậy, m' là một số tự nhiên. Điều này cho thấy rằng m chia hết cho 121 và m là một bội số của 121.
Để tìm tổng tất cả các số tự nhiên có hai chữ số không chia hết cho 3 và 5, chúng ta cần tìm tổng của tất cả các số tự nhiên từ 10 đến 99 không chia hết cho 3 và 5.Để tính tổng này, chúng ta có thể sử dụng công thức tổng của một dãy số từ một số đến một số khác. Công thức này là:
Tổng = (Số lượng số trong dãy) * (Tổng của số đầu tiên và số cuối cùng) / 2,
trong đó, Số lượng số trong dãy = (Số cuối cùng - Số đầu tiên) + 1.
Áp dụng công thức này vào bài toán, ta có:
Số đầu tiên = 10, Số cuối cùng = 99, Số lượng số trong dãy = (99 - 10) + 1 = 90.
Tổng = 90 * (10 + 99) / 2 = 90 * 109 / 2 = 90 * 54,5 = 4.905.
Vậy tổng tất cả các số tự nhiên có hai chữ số không chia hết cho 3 và 5 là 4.905.
Đúng 0
Bình luận (0)
Bài 4. 1) Cho hai số tự nhiên a và b thỏa mãn số: m=(16a+17b)(17a+16b) là một bội số của 11. Chứng minh rằng số m cũng là một bội số của 121 2) Tìm tổng tất cả các số tự nhiên có hai chữ số không chia hết cho 3 và 5
Bài toán 1: Để chứng minh số m cũng là một bội số của 121, ta sẽ sử dụng một số tính chất của phép chia.
Ta có: m = (16a + 17b)(17a + 16b) = (17a + 16b)^2 - (ab)^2
Vì m là một bội số của 11, nên ta có thể viết m dưới dạng m = 11k, với k là một số tự nhiên.
Từ đó, ta có (17a + 16b)^2 - (ab)^2 = 11k.
Áp dụng công thức (a + b)^2 - (ab)^2 = (a - b)^2, ta có (17a + 16b + ab)(17a + 16b - ab) = 11k.
Ta có thể chia hai trường hợp để xét:
Trường hợp 1: (17a + 16b + ab) chia hết cho 11. Trường hợp 2: (17a + 16b - ab) chia hết cho 11.
Trong cả hai trường hợp trên, ta đều có một số tự nhiên tương ứng với mỗi trường hợp.
Do đó, nếu m là một bội số của 11, thì m cũng là một bội số của 121.
Bài toán 2: Để tìm tổng tất cả các số tự nhiên có hai chữ số không chia hết cho 3 và 5, ta cần xác định tập hợp các số thỏa mãn điều kiện trên và tính tổng của chúng.
Các số tự nhiên hai chữ số không chia hết cho 3 và 5 có dạng AB, trong đó A và B lần lượt là các chữ số từ 1 đến 9.
Ta thấy rằng có 3 chữ số (3, 6, 9) chia hết cho 3 và 2 chữ số (5, 0) chia hết cho 5. Vì vậy, số các chữ số không chia hết cho 3 và 5 là 9 - 3 - 2 = 4.
Do đó, mỗi chữ số A có 4 cách chọn và mỗi chữ số B cũng có 4 cách chọn.
Tổng tất cả các số có hai chữ số không chia hết cho 3 và 5 là 4 x (1 + 2 + 3 + ... + 9) x 4 = 4 x 45 x 4 = 720.
Vậy tổng tất cả các số tự nhiên có hai chữ số không chia hết cho 3 và 5 là 720.
Đúng 0
Bình luận (0)
Tổng hai số tự nhiên a;b thỏa mãn \(\left(a+1\right)^2+\left(b-2\right)^2=4\) là ?
Ta có: 4 = 0 + 4 = 1 + 3 = 2 + 2 mà (a+1)^2, (b-1)^2 phải khác 2 và 3. do a, b là số tự nhiên
Vậy ta có:
| (a+1)^2 | 0 | 4 |
| a | -1 | 1 |
| (b-1)^2 | 4 | 0 |
| b | 3 | 1 |
vậy (a+1)^2 + (b-1)^2 = 0 + 4 = 4 khi a + b = 1 + 1 = 2
(a+1)^2 + (b-1)^2 = 4 + 0 = 4 khi a + b = -1 + 3 = 2
Đúng 0
Bình luận (0)
Hai số tự nhiên a và b, thỏa mãn: a – b 50 và phân số a/b 5/3 Là:
Đọc tiếp
Hai số tự nhiên a và b, thỏa mãn: a – b = 50 và phân số a/b = 5/3 Là:
Ta có sơ đồ:
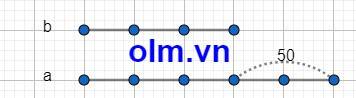
Theo sơ đồ ta có:
Số a là: 50 : (5-3) x 5 = 125
Số b là: 125 - 50 = 75
Đs..
Đúng 1
Bình luận (0)



















