Giải phương trình sau: ( 1 + sinx + cos 2 x ) sin x + π 4 1 + tanx = 1 2 cosx
A. x = - π 6 + k2π
B. x = - 5 π 3 + k π 2
C. x = - π 6 + k2π; 7 π 6 + k2π
D: Đáp án khác
Giải phương trình sau: 1 - 2 sinx cosx ( 1 + 2 sinx ) ( 1 - sinx ) = 3
A. x = - π 18 + kπ
B. x = - π 18 + k 2 π 3
C. x = - π 6 + kπ; - π 18 + kπ
D: Đáp án khác
Giải phương trình sau: 5sinx – 2 = 3(1 – sinx)tan2x
A. x = π 6 + k2π
B. x = 5 π 6 + kπ
C. x = - 5 π 6 + kπ, kπ
D. Đáp án khác.
Giải phương trình sau: cosx ( cosx + 2 sinx ) + 3 sinx ( sinx + 2 ) sin 2 x - 1 = 1
A. x = - π 4 + k2π
B. x = - 3 π 4 + k2π
C. x = ± π 4 + kπ
D. Cả A và B đúng
Giải phương trình sau: sin 2 x + 2 cosx - sinx - 1 tanx + 3 = 0
A. x = π 3 + k2π
B. x = - π 3 + k π 2
C. x = π 3 + k2π; - π 3 + k2π
D: Đáp án khác
Giải các phương trình sau:
1. F'(x)=0 với y(x)=3x+60/x -64/x^3+5
2. F'(x)=0 với f(x)=1-sin(pi+x)+2cos((3pi+x)/2)
3. F'(x)=0 với f(x)=sin3x/3 +cosx -√3*(sinx+(cos3x/3))
4. G'(x)=0 với g(x)=sin3x -√3*cos3x +3*(cosx -√3*sinx)
Giải phương trình sau: 1 + sin 2 x + cos 2 x 1 + cot 2 x = 2 sinx . sin 2 x
A. x = - π 4 + k2π
B. x = - π 4 + k π 2
C. x = π 2 + kπ; π 4 + k2π
D. x = π 2 + kπ
Giải phương trình sau: 2 3 sin x - π 8 cos x - π 8 + 2 cos 2 x - π 8 = 3 + 1
A. 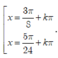
B. 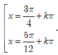
C. 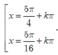
D: 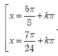
Giải phương trình sau
|x^2 +2014|=1
Mn giải giúp mk vs
\(x^2\ge0\)
\(\Rightarrow\)\(x^2+2014\ge2014\)
\(\Rightarrow\)\(\left|x^2+2014\right|=x^2+2014\)
Vậy ta có: \(x^2+2014=1\)
\(\Leftrightarrow\) \(x^2=-2013\) vô lí
Vậy pt vô nghiệm
Vì x2+2014>0 với mọi x => \(|x^2+2014|=x^2+2014\ge2014\)
\(\Rightarrow\)Đẳng thức ở đề bài không thể xảy ra
chị bỏ giá trị tuyệt đối ra .th 1 lấy 1-2014=-2013.tinh căn bậc 2 của -2013
th2 lấy-1 -2014=-2015.tìm căn bậc 3 của-2015x
x sẽ có 2 th và 2 kết ủa khác nhau
Giải hệ phương trình sau
\(\left\{{}\begin{matrix}x^2+y^2+6x+2y=0\\x+y+8=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+\left(x+8\right)^2+6x-2\left(x+8\right)=0\\y=-x-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+10x+24=0\\y=-x-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=-4\\x=-6\end{matrix}\right.\\y=-x-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-4\\y=-4\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=-2\end{matrix}\right.\end{matrix}\right.\)
Kết luận: Hệ phương trình đã cho có nghiệm \(\left(x;y\right)\in\left\{\left(-4;-4\right);\left(-6;-2\right)\right\}\)