Trong mp Oxy, cho đường tròn (C): x 2 + y 2 – 4x + 2y + 1 = 0. Phương trình của đt (C’) đối xứng với (C) qua trục hoành
A. x 2 + y 2 + 4 x − 2 y + 1 = 0
B. x 2 + y 2 − 4 x − 2 y + 1 = 0
C. x 2 + y 2 + 4 x + 2 y + 1 = 0
D.Đápán khác
Những câu hỏi liên quan
Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C) : x2 + y2 – 2x + 2y + 1 0Phương trình đường tròn (C’) đối xứng (C) qua trục tung là: A.
(
x
−
1
)
2
+
(
y
−
1
)
2
1
B.
(
x...
Đọc tiếp
Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C) : x2 + y2 – 2x + 2y + 1 = 0
Phương trình đường tròn (C’) đối xứng (C) qua trục tung là:
A. ( x − 1 ) 2 + ( y − 1 ) 2 = 1
B. ( x + 1 ) 2 + ( y − 1 ) 2 = 2
C. ( x + 1 ) 2 + ( y + 1 ) 2 = 2
D. ( x + 1 ) 2 + ( x + 1 ) 2 = 1
Đáp án D
(C) có tâm I( 1; – 1), bán kính 1
Đ O y : I => I’( – 1; – 1 )
Phương trình đường tròn (C’): ( x + 1 ) 2 + ( y + 1 ) 2 = 1
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho điểm A(4; – 1), đường thẳng (d) : 3x – 2y + 1 = 0 và đường tròn (C) :
x^2 + y^2 - 2x + 4y -4 = 0
a. Tìm tọa độ A’ và phương trình (d’) lần lượt là ảnh của A và (d) qua phép tịnh tiến theo vectơ v = (– 2; 3)
b. Tìm phương trình đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng trục là đường thẳng (D) : x – y = 0
trong mặt phẳng oxy viết phương trình đường tròn (c) có tâm nằm trên trục hoành và đường tròn (c) tiếp xúc với cả hai đường thẳng (d1):2x-y-1=0 (d2):x-2y+1=0 Trong mặt phẳng Oxy,viết phương trình đường tròn
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình \(3x+2y-6=0\) và đường tròn (C) có phương trình \(x^2+y^2-2x+4y-4=0\). Tìm ảnh của M, d và (C) qua phép đối xứng qua trục Ox ?
Trong mặt phẳng Oxy cho đường tròn (C):
x
−
1
2
+
y
−
2
2
9
. Viết phương trình đường tròn ảnh của đường tròn đã...
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn (C): x − 1 2 + y − 2 2 = 9 . Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép đối xứng trục d: x = 1.
Chỉ cần tìm ảnh của tâm đường tròn qua trục d.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x − 2y – 6 0a) Viết phương trình của đường thẳng
d
1
là ảnh của d qua phép đối xứng qua trục Oyb) Viết phương trình của đường thẳng
d
2
là ảnh của d qua phép đối xứng qua đường thẳng Δ có phương trình
x
+
y
–
2
0
.
Đọc tiếp
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x − 2y – 6 = 0
a) Viết phương trình của đường thẳng d 1 là ảnh của d qua phép đối xứng qua trục Oy
b) Viết phương trình của đường thẳng d 2 là ảnh của d qua phép đối xứng qua đường thẳng Δ có phương trình x + y – 2 = 0 .
a) d 1 : 3x + 2y + 6 = 0
b) Giao của d và Δ là A(2;0). Lấy B(0; −3) thuộc d. Ảnh của B qua phép đối xứng của đường thẳng Δ là B′(5;2). Khi đó d' chính là đường thẳng AB′: 2x − 3y – 4 = 0
Đúng 0
Bình luận (0)
Câu 26. Cho hai đường tròn (C):(x-2)^ 2 +(y-2)^ 2 =9;(C' ):x^ 2 +y^ 2 +4x-8y+11=0 ,biết (C) và (C') đối xứng nhau qua đường thẳng (a) .Phương trình của (a) là : A. 2x + 2y - 4 = 0 B.2x-y+3=0 . C. x + y - 4 = 0 . D. 2x + 2y = 0 .
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình:
x
2
+
y
2
-
4
x
+
5
y
+
1
0
. Phép đối xứng trục Oy biến (C) thành (C’) có phương trình: A.
x
2
+
...
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: x 2 + y 2 - 4 x + 5 y + 1 = 0 . Phép đối xứng trục Oy biến (C) thành (C’) có phương trình:
A. x 2 + y 2 - 4 x – 5 y + 1 = 0
B. x 2 + y 2 + 4 x + 5 y + 1 = 0
C. x 2 + y 2 - 4 x + 5 y + 1 = 0
D. x 2 + y 2 + 4 x – 5 y + 1 = 0
Phép đối xứng qua trục Oy có :
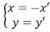
Thay vào phương trình (C) ta được x ' 2 + y ' 2 + 4 x ' + 5 y ' + 1 = 0 hay x 2 + y 2 + 4 x + 5 y + 1 = 0
Đáp án B
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 0 và đường tròn (C) có phương trình
x
2
+
y
2
−
2
x
+
4
y
–
4
0
. Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 = 0 và đường tròn (C) có phương trình x 2 + y 2 − 2 x + 4 y – 4 = 0 . Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox .
Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
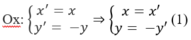
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0.
Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x ' 2 + y ' 2 − 2 x ′ + 4 y ′ − 4 = 0 .
Từ đó suy ra phương trình của (C') là x − 1 2 + y − 2 2 = 9 .
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3,
từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là x − 1 2 + y − 2 2 = 9
Đúng 0
Bình luận (0)