Cho tam giác ABC, trên BC lấy M bất kì. Qua M kẻ ME//AC CE thuộc AB ; MF//AB (F thuộc AC). Gọi I là trung điểm AM.
Chứng Minh: E đối xứng với F qua I.

Những câu hỏi liên quan
Cho tam giác ABC cân tại A, lấy điểm D bất kì thuộc AB. Trên tia AC lất điểm E sao cho BD=CE. BC cắt DE tại M.
CMR: MD=ME
Cho tam giác ABC có 2 đường phân giác BD và CE (D thuộc AC, E thuộc AB). Trên ED lấy điểm M bất kì, lấy L,K,H lần lượt thuộc AB,AC,BC sao cho MH ⊥ BC, ML ⊥ AB, MK ⊥ AC. chứng minh MH = ML + MK
Cho tam giác ABC. Gọi M là điểm bất kì trên cạnh AC, qua M kẻ các đường thẳng ME, MF lần lượt song song với các cạnh AB, BC (E thuộc BC và F thuộc AB). Tìm vị trí của M để dt tứ giác BEMF có dt lớn nhất.
Tứ giác BEMF là hình bình hành ( hai cặp cạnh đối song song) |
Kẻ AH vuông góc BC tại H , AH cắt MF tại G. Ta có diện tích ABC=1/2AH*BC và S bemf=fm*gh nên Sbemf/Sabc=2*HG/AH*FM/BC |
Gọi AM = x; MC = y thìAC = x + y Xét tam giácABC có MF // BC (gt)FM/BC=AM/AC ( hệ quả định lí Talet) Thì FM/BC=x/x+y |
Xét tam giácAHC có GM //HCthì HG/AH=CM/AC ( định lí Talet) HG/AH=x/x+y |
Do đó Sbefm/Sabc=2*xy/(x+y)^2 Ta có : (x-y)^2>=0thif(x+y)^2>=4xy thì xy/(x+y)^2<=1/4 |
Sbemf/Sabc<=2*1/4hay Sbemf<=1/2Sabc |
Mà Sabc không đổi nên Sbemf đạt giá trị lớn nhất là 1/2Sabc khi và chỉ khi x=y Hay M là trung điểm của AC. Gõ mỏi tay ko biết đc j ko-_- |
Đúng 2
Bình luận (0)
Cho tam giác abc vuông cân tại a
AH là đường cao
Lấy M bất kì trên BC , qua M kẻ MD//AC , ME // AB
Chứng minh góc DEH bằng 45 độ
Cho tam giác ABC, một điểm M bất kì trên cạnh BC. Kẻ MD//AB, ME//AC (D ∈ AC, E ∈ AB). Gọi F là giao điểm BD và CE. Chứng minh SADFE = S ΔBFC
Cho tam giác ABC cân A, BH vuông góc AC tại H. Trên BC lấy M bất kì ( M thuộc BC). Gọi D,E,F là chân đường vuông góc kẻ từ M đến AB,AC, BH
a) CMR: Tam giác DBM = Tam giácFMB
b) CMR: Khi M chạy BC thì MD + ME có giá trị không đổi
c) Trên tia đối tia CA lấy K sao cho CK=EH. CMR: BC đi qua trung điểm BK
cho tam giác abc, m là một điểm bất kì trên cạnh ab. qua m kẻ me//bc; mb//ac, e thuộc ac, f thuộc ab.
a) chứng minh tứ giác cèm là hình bình hành.
b) với điều kiện nào của tam giác abc và điểm m thì tứ giác cèm là hình chữ nhật, hình thoi, hình vuông?
Giúp mình với ạ !
Từ điểm M bất kì trên cạnh BC của tam giác ABC vuông tại A , kẻ MD // AB ( D thuộc AC ) , ME // AC ( E thuộc AB ) . Xác định vị trí của M trên BC để DE ngắn nhất
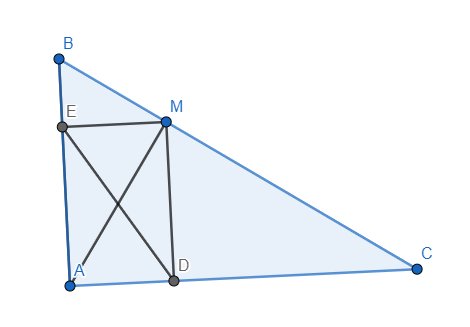
Do MD//AB và \(AB\perp AD\) nên \(MD\perp AD\) hay \(\widehat{ADM}=90^o\). Hoàn toàn tương tự, ta có \(\widehat{AEM}=90^o\). Mà \(\widehat{DAE}=90^o\) nên tứ giác ADME là hình chữ nhật. Do đó \(DE=AM\). Như vậy, ta quy về tìm vị trí của M trên BC để AM nhỏ nhất. Kẻ đường cao AH của tam giác ABC thì H cố định. Ta thấy AH và AM lần lượt là đường vuông góc và đường xiên kẻ từ A lên BC nên \(AM\ge AH\). Dấu "=" chỉ xảy ra khi \(M\equiv H\) hay M là chân đường vuông góc hạ từ A lên BC.
Đúng 2
Bình luận (0)
Cho tam giác ABC có AB AC BC m m 0 . Trên cạnh Bc lấy D sao cho BD 1 3 BC. Từ D kẻ DE vuông góc BC tại D E thuộc AB , kẻ DF vuông góc AC tại F .a Chứng minh tam giác DEF đềub Lấy điểm M bất kì trên cạnh BC , từ M kẻ MH vuông góc AB tại H, MK vuông góc AC tại K .Tính MH MK 2














