Mình vào rùi nè

giải rồi đó bn

mình giải nè

tich ủng hộ nha các bạn

mik cần cách làm, làm ơn trình bày rõ cho mik

Cách đăng ký tài khoản OLM, luyện giải Toán trên olm.vn

Đóng góp bởi Đặng Thái Đức21/01/2021

OLM.vn là trang web học trực tuyến, nơi mà các em học sinh có thể học tập, ôn luyện và bổ sung thêm các kiến thức bộ môn Toán từ cấp độ Tiểu Học cho đến Trung Học Phổ Thông. Trong bài viết này, mình sẽ hướng dẫn cách tạo tài khoản, luyện giải toán trên olm.vn.

Xem nhanh

I. OLM là gì? Lợi ích việc học, ôn luyện Toán trên olm.vnII. Hướng dẫn đăng ký tài khoản OLM, luyện giải Toán trên olm.vn1. Hướng dẫn nhanh2. Hướng dẫn chi tiết

Cách đăng ký tài khoản OLM, luyện giải Toán trên olm.vn

I. OLM là gì? Lợi ích việc học, ôn luyện Toán trên olm.vn

OLM.vn là trang web học trực tuyến (trực thuộc Trường Đại học Sư phạm Hà Nội), nơi mà các em học sinh có thể học tập, ôn luyện và bổ sung thêm các kiến thức bộ môn Toán, Tiếng Việt, Tiếng Anh, Vật lí, Hóa học, Lịch sử, Địa Lý từ cấp độ Tiểu Học cho đến Trung Học Phổ Thông.

OLM.vn

Lợi ích:

Cung cấp chương trình học từ lớp 1 đến lớp 12 với các môn Toán, Tiếng Việt, Tiếng Anh, Vật lí, Hóa học, Lịch sử, Địa LýCó chuyên mục giải toán có đáp số, lời giải rõ ràngCó các bài kiểm tra để báo cáo điểm cho học sinh

II. Hướng dẫn đăng ký tài khoản OLM, luyện giải Toán trên olm.vn

Hướng dẫn sau đây được thực hiện trên điện thoại iPhone XS chạy hệ điều hành iOS. Tuy nhiên, bạn cũng có thể thực hiện thao tác tương tự trên điện thoại Android, máy tính hệ điều hành Windows, macOS.

1. Hướng dẫn nhanh

Vào trang web https://olm.vn/ > Chọn Đăng ký > Nhập họ tên của bạn, đặt tên tài khoản, mật khẩu, nhập địa chỉ email > Nhập mã xác minh > Nhấn Đăng ký tài khoản > Đăng nhập bằng tên tài khoản, mật khẩu vừa tạo > Chọn khối lớp muốn học > Chọn môn học > Chọn bài học Chọn Video để xem video bài giảngChọn Luyện tập để luyện giải bài tập > Điền số vào ô kết quả tương ứng > Nhấn Nộp bài > Hiển thị lời giải chính xác

2. Hướng dẫn chi tiết

Bước 1: Vào trang web https://olm.vn/ > Chọn Đăng ký

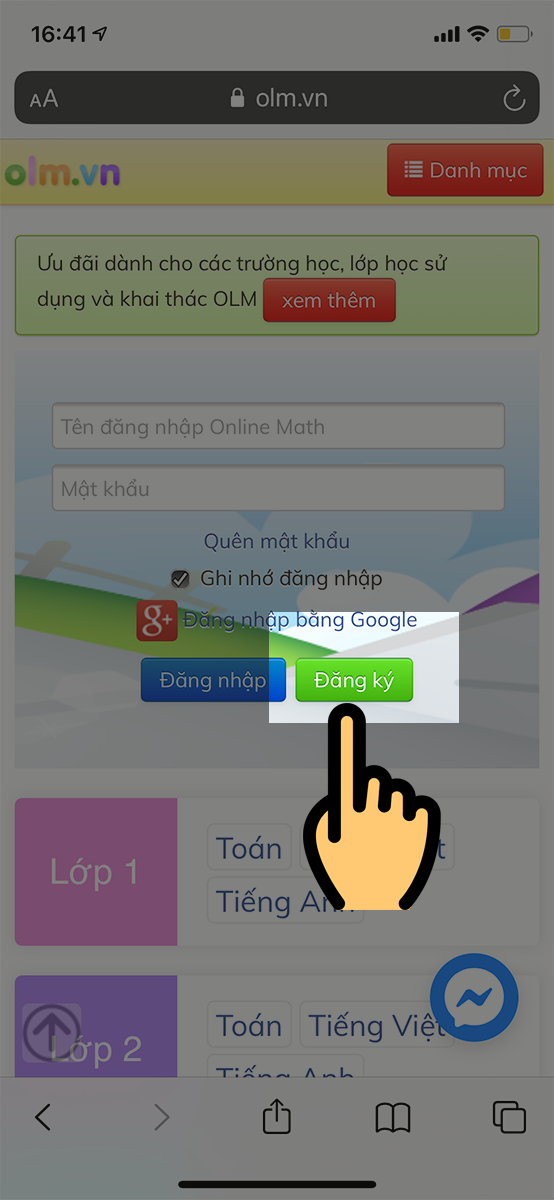
Chọn Đăng ký

Bước 2: Nhập họ tên của bạn, đặt tên tài khoản, mật khẩu, nhập địa chỉ email > Nhập mã xác minh các chữ cái trong hình > Nhấn Đăng ký tài khoản

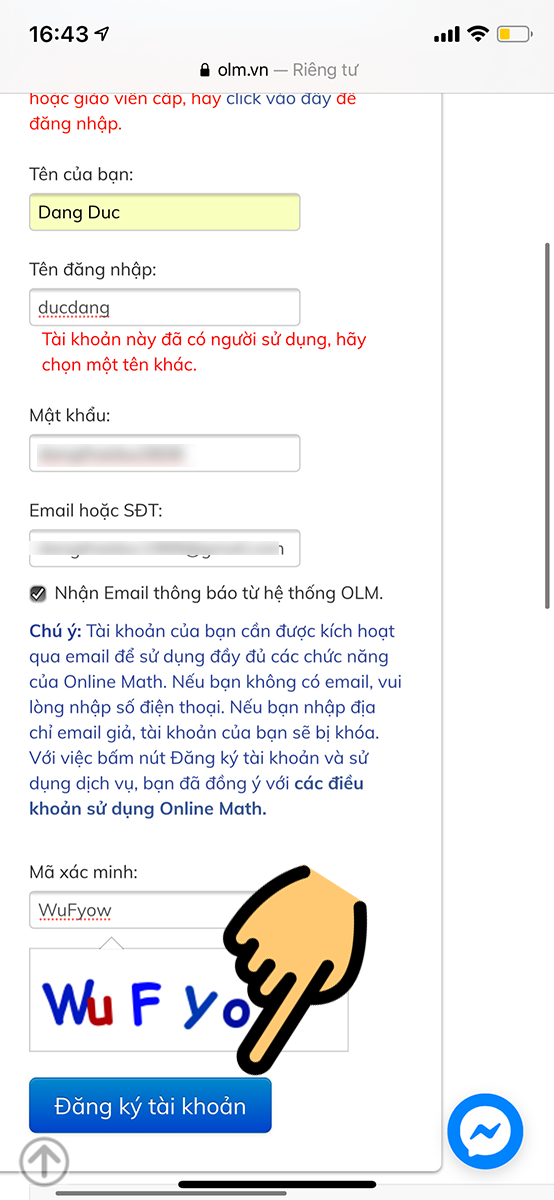
đặt tên tài khoản, mật khẩu

Bước 3: Hệ thống chuyển bạn đến trang đăng nhập > Đăng nhập bằng tên tài khoản, mật khẩu vừa tạo

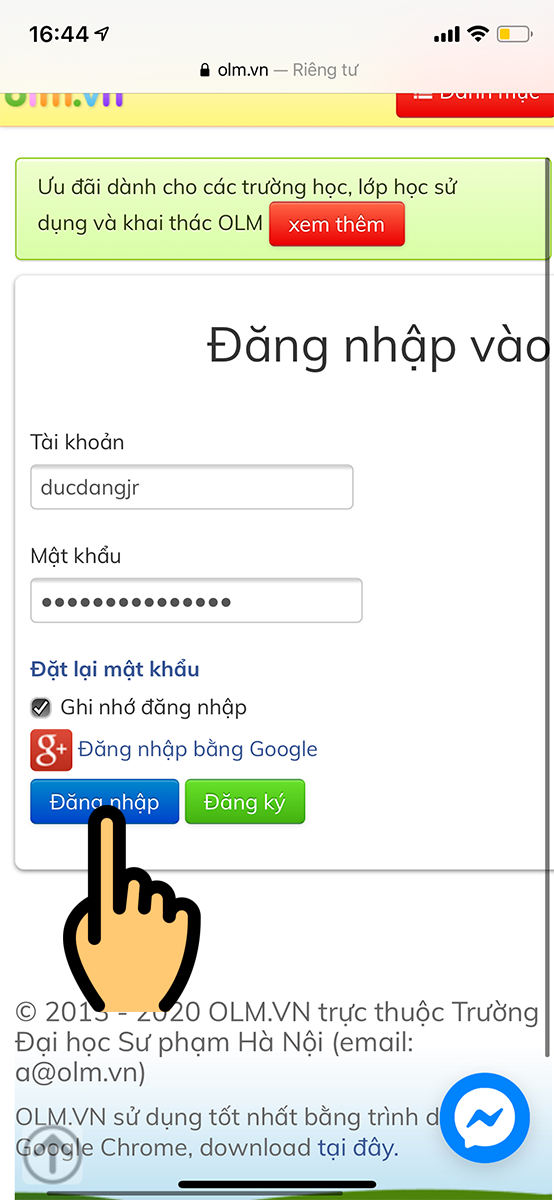
Đăng nhập bằng tên tài khoản, mật khẩu

Bước 4: Chọn khối lớp muốn học > Chọn môn học

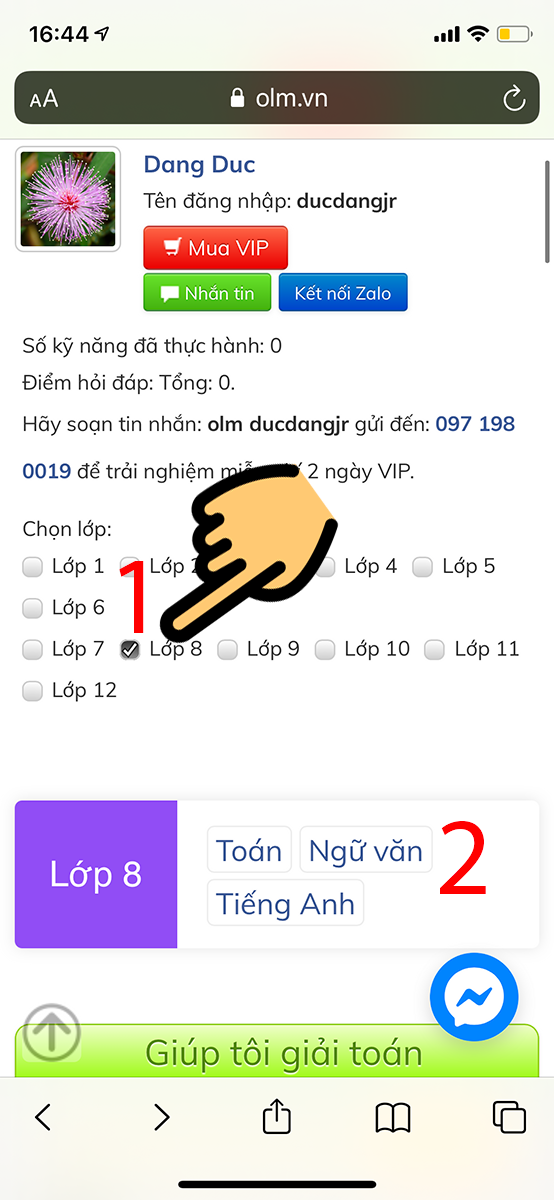
Chọn khối lớp muốn học

Bước 5: Chọn bài học 

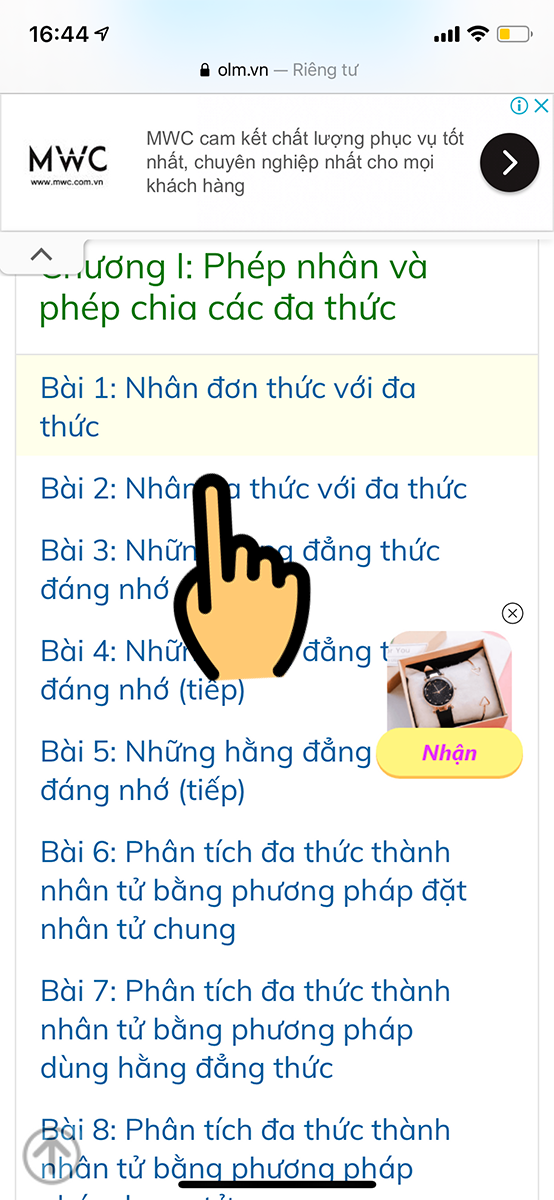
Chọn bài học 

Bước 6: Chọn Video để xem video bài giảng

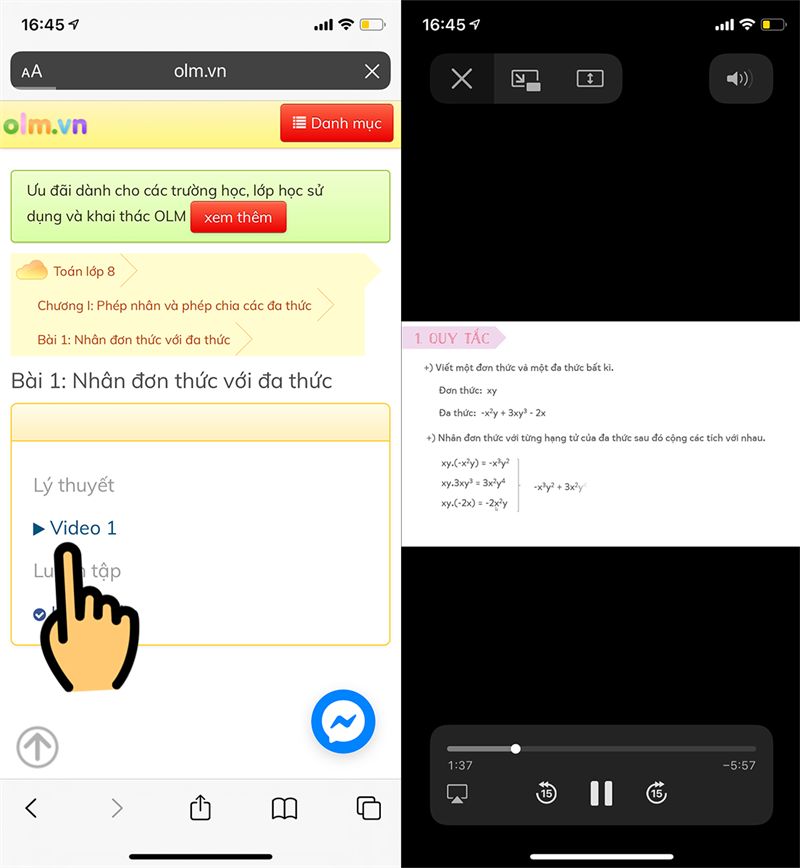
Chọn Video để xem video bài giảng

Bước 7: Chọn Luyện tập để luyện giải bài tập > Điền số vào ô kết quả tương ứng > Nhấn Nộp bài > Hiển thị lời giải chính xác

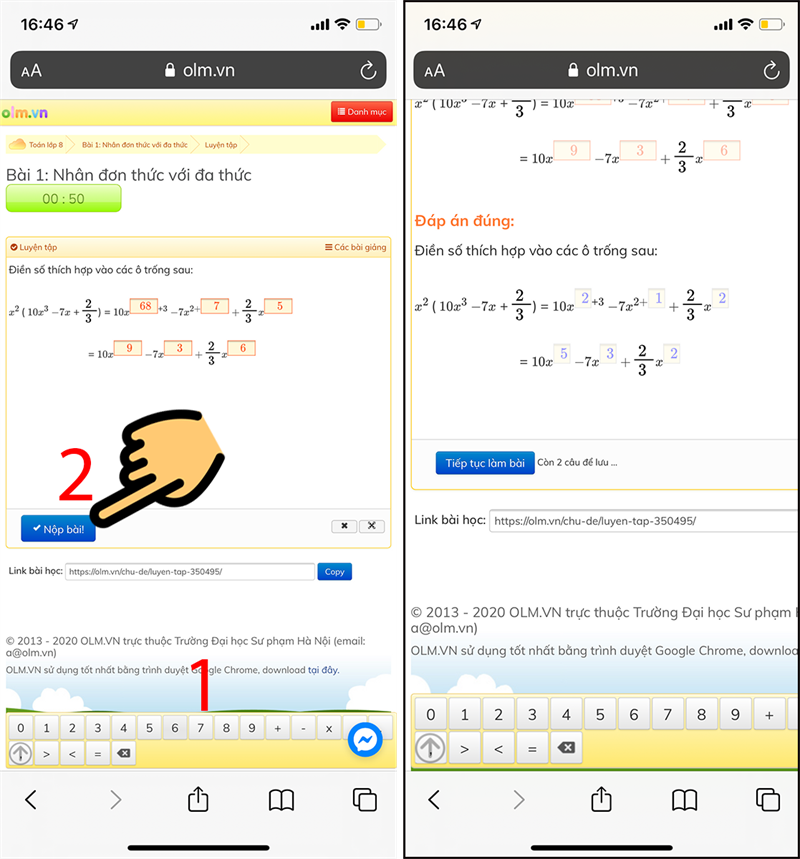
Chọn Luyện tập để luyện giải bài tập

Lời giải đã được đăng ở đấy, post lại ở đây cho bạn dễ tìm

 

Để giải bài toán này đầu tiên ta có một nhận xét: Với mọi số dương \(x>0\) thì \(2x^3\ge3x^2-1.\)  Thực vậy xét hiệu hai vế ta có \(2x^3-3x^2+1=\left(x-1\right)^2\left(2x+1\right)\ge0.\)

Bây giờ, gọi \(D,E,F\)  là chân các đường cao kẻ từ \(A,B,C\).  Theo hệ thức lượng trong tam giác vuông (liên hệ giữa cạnh và hình chiếu) ta có:   Đối với tam giác vuông \(\Delta A'BC\)  và đường cao \(A'D\)  thì \(\frac{A'B^2}{A'C^2}=\frac{DB}{DC}\). Tương tự ta cũng có \(\frac{B'C^2}{B'A^2}=\frac{EC}{EA},\frac{C'A^2}{C'B^2}=\frac{FA}{FB}.\)  Suy ra  \(\frac{A'B^2}{A'C^2}+\frac{B'C^2}{B'A^2}+\frac{C'A^2}{C'B^2}=\frac{DB}{DC}+\frac{EC}{EA}+\frac{FA}{FB}\)

Vì ba đường cao đồng quy nên theo định lý Ceva  \(\frac{DB}{DC}\cdot\frac{EC}{EA}\cdot\frac{FA}{FB}=1\).  Do đó theo bất đẳng thức Cô-Si ta được

\(\frac{DB}{DC}+\frac{EC}{EA}+\frac{FA}{FB}\ge3\sqrt[3]{\frac{DB}{DC}\cdot\frac{EC}{EA}\cdot\frac{FA}{FB}}=3.\)  Vì vậy mà \(\frac{A'B^2}{A'C^2}+\frac{B'C^2}{B'A^2}+\frac{C'A^2}{C'B^2}\ge3.\)

Từ đó áp dụng Nhận xét ta thu được \(2\left(\frac{A'B^3}{A'C^3}+\frac{B'C^3}{B'A^3}+\frac{C'A^3}{C'B^3}\right)\ge3\left(\frac{A'B^2}{A'C^2}+\frac{B'C^2}{B'A^2}+\frac{C'A^2}{C'B^2}\right)-3\ge3\cdot3-3=6.\)

Vì vậy ta được \(\frac{A'B^3}{A'C^3}+\frac{B'C^3}{B'A^3}+\frac{C'A^3}{C'B^3}\ge3.\) 

Dấu bằng xảy ra khi và chỉ khi D,E,F là trung điểm ba cạnh AB,BC,CA và điều đó có nghĩa là tam giác ABC đều.

Nhớ thanks nhé!