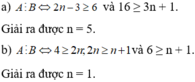2n+7 chia hết cho n-2

suy ra 2(n-2)+4+7 chia hết cho n-2

suy ra 2(n-2)+11 chia hết cho n-2

có 2(n-2) chia hết cho n-2

suy ra 11 chia hết cho n-2

suy ra n-2 thuộc Ư(11)= 1;11;-1;-11

mà n là số nguyên dương 

suy ra n thuộc tập hợp 3;13;1

Có 2n+7 chia hết cho n-2

=>2(n-2)+11 chia hết cho n-2

=>11 chia hết cho n-2

=>n-2 thuộc Ư(11)={1;11}

Với n-2=1   =>n=3

Với n-2=11 =>n=13

Vậy n thuộc {3;13}

n^2 +2n+6 chia hết cho n+4

tìm nghiệm của bt chia(n+4)

ta tìm được nghiệm là -4

thế nghiệm và bt bị chia

=>(-4)^2+(-4).2+6=14

=.n+4 là ước của 14=(-14,-7,-2,-1,2,7,14)

n+4=-14=>n=-18(loại vì n>0)

n+4=-7=>n=-11(loại)

n+4=-2=>n=-6(loại)

n+4=-1=>n=-5(loại)

n+4=1=>n=-3(loại)

n+4=2=>n=-2(loại)

n+4=7=>n=3(nhận)

n+4=14=>n=10(nhận)

vậy n=3;10

A = ( n + 5 ) ( n + 2 ) = n² + 7n + 10 

A : 6n = \(\frac{\left(n^2+7n+10\right)}{6n}=\frac{1}{6}\left(n+\frac{10}{n}+7\right)\)

Để A chia hết cho 6n

thì  \(n+\frac{10}{n}+7\) chia hết cho 6

=> \(n+\frac{10}{n}+7\in B\left(6\right)\)(1)  và  \(n\inƯ\left(10\right)\)(2)

Giải ( 2) ta có: n là số nguyên dương 

=> n \(\in\){ 1; 2; 5; 10 }

Với n = 1, ta có: \(n+\frac{10}{n}+7=1+10+7=18\) chia hết cho 6 => n = 1 thỏa mãn

Với n = 2 ta có: \(n+\frac{10}{n}+7=2+\frac{10}{5}+7=11\)không chia hết cho 6 => loại

Với n = 5 ta có: \(n+\frac{10}{n}+7=5+\frac{10}{5}+7=14\)không chia hết cho 6 => loại

Với n = 10  ta có: \(n+\frac{10}{n}+7=10+\frac{10}{10}+7=18\) chia hết cho 6 => n = 10 thỏa mãn

Vậy n \(\in\){ 1; 10 }

https://olm.vn/hoi-dap/detail/195347678157.html