cho tam giác ABC vuông tại A , AB=3cm,BC=7,8cm.Gọi BD và BE là các đường phân giác góc trong và góc ngoài của góc B ( D và E thuộc AC ) . Tính DE
giúp mình với !!!!
Cho tam giác ABC vuông tại A; AB = 6; BC=10. Đường phân giác trong của góc B cắt AC tại D; đường phân giác ngoài của góc B cắt AC tại E. Tính BD và BE
Bài 1: Cho tam giác ABC có góc A = 70*. Tia phân giác của B cắt tia phân giác của C ở I và cắt đường phân giác của góc ngoài tại C ở K. Tính góc BIC và góc BKC.
Bài 2: Cho tam giác ABC vuông góc tại A, kẻ đường cao AH. Tia phân giác của góc A cắt BC tại D. Biết góc DAH = 15*. Tính các góc của tam giác ABC.
Bài 3: Cho tam giác ABC có góc A, B, C là góc nhọn, góc A = 50*. Qua B kẻ đoạn thẳng BD vuông góc với AC (D thuộc AC). Qua C kẻ CE vuông góc với AB (E thuộc AB). Gọi H là giao điểm của BD và CE.
a) Tính góc ABD và góc ACE.
b) Tính góc DHE.
Cho tam giác ABC cân tại a , Kẻ BD Vuông góc AC , CE Vuông góc AV ( D Thuộc AC, E thuộc AB Gọi O là giao Điểm Của BD Và CE. Chứng Minh a) BD=CE; b) Tam Giác OEB = Tam giác ODC c) AO là tia phân giác của góc BAC ; d) Cho biết BE = 3cm ; BC=5cm.Tính BD?
Ai trả lời giúp mình với mình đang cần gấp
a) Vì tam giác ABC cân tại a (GT)
=> góc ABC = góc ACB (ĐL) hay góc EBC = góc DCB (1)
Vì BD vuông góc với AC (GT) => Góc BDC = 90 độ (ĐN) (2)
Vì CE vuông góc với AB (GT) => Góc CEB = 90 độ (ĐN) (3)
Từ (2), (3) => Góc BDC = góc CEB = 90 độ (4)
Xét tam giác BEC và tam giác CDB có :
Góc BDC = góc CEB = 90 độ (Theo (4))
BC chung
góc EBC = góc DCB (Theo (1))
=> tam giác BEC = tam giác CDB (ch - gn) (5)
=> CE = BD (2 cạnh tương ứng)
b) Từ (5) => BE = CD (2 cạnh tương ứng) (6)
Từ (5) => Góc BCE = góc CBD (2 góc tương ứng) (7)
Mà góc BCE + góc ACE = góc ACB
góc CBD + góc ABD = góc ABC
góc ACB = góc ABC (Theo (1))
Ngoặc '}' 4 điều trên
=> Góc ACE = góc ABD hay góc DCO = góc EBO (8)
Xét tam giác BEO và tam giác CDO có :
Góc BEO = góc CDO = 90 độ (Theo (4))
BE = CD (Theo (6))
Góc EBO = góc DCO (Theo (8))
=> tam giác OEB = tam giác ODC (g.c.g) (9)
c) Từ (9) => OB = OC (2 cạnh tương ứng) (10)
Vì tam giác ABC cân tại A (GT) => AB = AC (ĐN) (11)
Xét tam giác ABO và tam giác ACO có :
AO chung
OB = OC (Theo (10))
AB = AC (Theo (11))
=> tam giác ABO = tam giác ACO (c.c.c)
=> Góc BAO = góc CAO (2 góc tương ứng)
Mà AO nằm giữa BO và CO
=> AO là tia pg của góc BAC (đpcm)
d) Ta có : BE = CD (Theo (6))
Mà BE = 3cm (GT)
=> CD = 3cm (12)
Xét tam giác BCD vuông tại D có :
BD2 + CD2 = BC2 (ĐL pi-ta-go)
Mà CD = 3cm (Theo (12))
BC = 5cm (GT)
=> BD2 + 32 = 52
=> BD2 + 9 = 25
=> BD2 = 25 - 9
=> BD2 = 16
=> BD2 = \(\sqrt{14}\)
=> BD = 4cm
Vậy a)... b)... c)... d)...
a/ Xét t/g vuông: t/g ABD và t/g ACE có:
AB = AC (gt)
Aˆ:chungA^:chung
=> t/g ABD = t/g ACE (cạnh huyền-góc nhọn)
=> BD = CE
b/ Vì AB = AC => t/g ABC cân tại A
=> ABCˆ=ACBˆABC^=ACB^
Xét 2 t/g vuông: t/g BEC và t/g CDB có:
BD = CE (ý a)
ABCˆ=ACBˆ(cmt)ABC^=ACB^(cmt)
=> t/g BEC = t/g CDB (cạnh góc vuông - góc nhọn kề)
=> BE = CD
Xét t/g OEB và t/g ODC có:
OEBˆ=ODCˆ=90o(gt)OEB^=ODC^=90o(gt)
BE = CD (cmt)
ABDˆ=ACEˆABD^=ACE^ (2 góc tương ứng do t/g ABD = t/g ACE)
=> t/g OEB = t/g ODC (g.c.g)
c/ xét t/g AOB và t/g AOC có:
AO: cạnh chung
AB = AC (gt)
OB = OC (2 cạnh tương ứng do t/g OEB = t/g ODC)
=> t/g AOB = t/g AOC (c.c.c)
=> OABˆ=OACˆOAB^=OAC^ (2 cạnh tương ứng)
=> AO là tia p/g của góc BAC
CHÚC BẠN HỌC TỐT
2) Cho tam giác ABC vuông tại A có AB= 6cm, BC= 10cm. Các đường phân giác trong và ngoài của góc B cắt BC tại D và E. Tính BD và BE
Bài 1: Cho tam giác ABC, có AB = 6cm, BC = 10cm. Các đường phân giác trong và ngoài của góc B cắt AC lần lượt tại D và E. Tính BD và BE.
Bài 2: Cho tam giác ABC vuông tại A, đường phân giác trong AD, đường cao AH, CD = 68cm, BD = 51cm. Tính BH
Cho tam giác ABC, góc A= 90 độ; biết AB=6cm, BC=10 cm . Các đường phân giác trong và ngoài góc B cắt AC lần lượt tại D và E. Tính BD, BE
Cách 1:
\(AC=\sqrt{BC^2-AB^2}=8\) cm
Từ D kẻ \(DH\perp BC\) tại H
Xét hai tam giác vuông DHB và DAB có:
\(\widehat{DBH}=\widehat{DBA}\) ( do BD là tia phân giác góc B)
BD chung
Nên \(\Delta DHB=\Delta DAB\left(ch-gn\right)\)
Suy ra \(HB=AB=6cm\Rightarrow HC=4cm\) và \(DH=DA\)
Áp dụng định lý pytago vào tam giác DHC vuông tại H có:
\(DC^2=4^2+DH^2\) \(\Leftrightarrow\left(AC-AD\right)^2=16+DA^2\)
\(\Leftrightarrow\left(8-AD\right)^2=16+AD^2\)
\(\Leftrightarrow AD=3\) \(\Rightarrow BD=\sqrt{AD^2+AB^2}=3\sqrt{5}\) cm
Cách 2:
\(\dfrac{DC}{DA}=\dfrac{BC}{BA}=\dfrac{10}{6}=\dfrac{5}{3}\)\(\Leftrightarrow\dfrac{DC}{5}=\dfrac{DA}{3}=\dfrac{DC+DA}{5+3}=\dfrac{AC}{8}=\dfrac{8}{8}=1\)
\(\Rightarrow DC=5,DA=3\)
Làm tương tự như trên
o. Tính BE
Có \(\dfrac{EA}{EC}=\dfrac{BA}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\Leftrightarrow\dfrac{EA}{EA+AC}=\dfrac{3}{5}\Leftrightarrow\dfrac{EA}{EA+8}=\dfrac{3}{5}\Leftrightarrow EA=12\)
\(BE=\sqrt{ED^2-BD^2}=\sqrt{\left(EA+AD\right)^2-BD^2}=6\sqrt{5}\) ( \(BE\perp BD\) do hai đường phân giác của hai góc kề bù)
Kết luận:...
cho tam giác ABC, AB= 3cm, AC=4cm, BC=5cm. a, chứng minh tam giác ABC vuông tại A. b, tính các góc các cạnh của tam giác ABC. c, phân giác của góc A cắt BC tại E, tính BE, CE. d, từ E kẻ EM và EN lần lượt vuông góc với AB và AC, hỏi tứ giác AMEN là hình gì, tính diện tích hình tứ giác AMEN
Xét tam giác ABC có :
\(bc^2\)=\(5^2\)=25
\(ab^2\)+\(ac^2\)=\(3^2\)+\(4^2\)=9+16=25
Suy ra:\(bc^2=ab^2+ac^2\)(định lí py-ta-go đảo)
Cho tam giác ABC, các đường phân giác của các góc ngoài tại B và C cắt nhau ở E. Gọi G, H, K theo thứ tự là chân đường vuông góc kẻ từ E đến các đường thẳng BC, AB, AC. Đường phân giác của góc ngoài tại A của tam giác ABC cắt các đường thẳng BE, CE tại D, F. Chứng minh rằng EA vuông góc với DF.
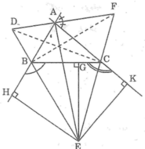
Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc ngoài tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.
Cho tam giác ABC vuông tại A có AB = 3cm, AC = 4cm.
a) Tính độ dài cạnh BC
b) Vẽ đường phân giác BD của tam giác ABC (D thuộc AC). Vẽ DE vuông góc BC tại E. Chứng minh tam giác ABD = tam giác EBD và Góc BED = 90 độ
c)Hai đường thẳng AB và ĐE cắt nhau tại F. Chứng minh BI là đường trung trực của EF
d) Gọi I là giao điểm của BD và FC. Chứng minh BI là đường trung trực của EF