Cho đường tròn đường kính AB, Cvaf D là 2 điểm khác nhau thuộc đường tròn (không trùng với A,B). Gọi E, F là các điểm thuộc đường tròn sao cho CE vuông góc với AD, DF vuông góc với AB. Chứng minh rằng CF, ED và AB đồng quy

Những câu hỏi liên quan
Cho đường tròn (O), đường kính BC. Lấy 1 điểm A trên đường tròn (O) sao cho ABAC. Từ A kẻ AH vuông góc vs BC( H thuộc BC). Từ H vẽ HE vuông góc với AB và HF vuông góc với AC (E thuộc AB và F thuộc AC).a, chứng minh rằng AEHF là hình chữ nhật và OA vuông góc với EFb, Đường thẳng EF cắt đường tròn tại P và Q (E nằm giữa P và F)Chứng minh AP^2AE*AB. suy ra APH là tam giác cânc, Gọi D là giao điểm của PQ và BC, K là giao điểm của AD và đường tròn (O) ( K khác A). Chứng minh rằng AEFK là tứ giác nộ...
Đọc tiếp
Cho đường tròn (O), đường kính BC. Lấy 1 điểm A trên đường tròn (O) sao cho AB>AC. Từ A kẻ AH vuông góc vs BC( H thuộc BC). Từ H vẽ HE vuông góc với AB và HF vuông góc với AC (E thuộc AB và F thuộc AC).
a, chứng minh rằng AEHF là hình chữ nhật và OA vuông góc với EF
b, Đường thẳng EF cắt đường tròn tại P và Q (E nằm giữa P và F)
Chứng minh AP^2=AE*AB. suy ra APH là tam giác cân
c, Gọi D là giao điểm của PQ và BC, K là giao điểm của AD và đường tròn (O) ( K khác A). Chứng minh rằng AEFK là tứ giác nội tiếp
d, Gọi I là giao điểm của KF và BC. Chứng minh IH^2=IC*ID
BÀI 1 cho nửa đường tròn tâm o đường kính AB CD là dây bất kì khác AB kẻ AE và BF vuông góc với CD chứng minh CEDFBÀI 2 cho nữa đường tròn O đường kính AB trên AB lấy hai điểm C và D sao cho OCOD .từ C và D kẻ hai tia song song nhau cắt nửa đường tròn tại E và F chứng minh EF vuông góc với CE và DFBài 3 cho đường tròn o có bán kính OA 11 cm điểm M thuộc OA và cách o là 7 cm qua M kẻ dây CD có độ dài 18 cm tính độ dài MC, MDBài 4 cho tam giác ABC cân nội tiếp đường tròn OA chừng minh AO là đường...
Đọc tiếp
BÀI 1 cho nửa đường tròn tâm o đường kính AB CD là dây bất kì khác AB kẻ AE và BF vuông góc với CD chứng minh CE=DF
BÀI 2 cho nữa đường tròn O đường kính AB trên AB lấy hai điểm C và D sao cho OC=OD .từ C và D kẻ hai tia song song nhau cắt nửa đường tròn tại E và F chứng minh EF vuông góc với CE và DF
Bài 3 cho đường tròn o có bán kính OA =11 cm điểm M thuộc OA và cách o là 7 cm qua M kẻ dây CD có độ dài 18 cm tính độ dài MC, MD
Bài 4 cho tam giác ABC cân nội tiếp đường tròn O
A chừng minh AO là đường trung trực của BC
B tính đường cao AH của tam giác ABC biết AC=40cm bán kình đường tròn O = 25 cm
Bài 5 cho đường tròn O đường kính AB dây CD vuông góc AB tại điểm M ,M thuộc OA
gọi I là một điểm thuộc OB .Các tia CI ,DI theo thứ tự cắt dường tròn tại E và F
A Cm tam giác ICD cân
gọi H,K theo thứ tự là chân các đường vuông góc kẻ từ O đến CE DF so sánh OH và OK
giúp mình với mình cảm ơn nhiều
Cho nửa đường tròn tâm O, đường kính AB. Qua điểm C thuộc nửa đường tròn kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ từ C đến AB. Chứng minh rằng : CE = CF
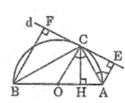
Ta có: OC ⊥ d (tính chất tiếp tuyến)
AE ⊥ d (gt)
BF ⊥ d (gt)
Suy ra : OC // AE // BF
Mà OA = OB (= R)
Suy ra: CE = CF (tính chất đường thẳng song song cách đều)
Đúng 0
Bình luận (0)
Cho ∆ABC nội tiếp đường tròn tâm O đường kính AB sao cho AC BC; E là một điểm thuộc đoạn BC (E khác B và C). Tia AE cắt đường tròn (O) tại điểm thứ hai D. Kẻ EH vuông góc với AB tại H.1) Chứng minh tứ giác ACEH là tứ giác nội tiếp.2) Tia CH cắt (O) tại điểm thứ hai F. Chứng minh rằng EH // DF.3) Chứng minh rằng đường tròn ngoại tiếp ∆CHO đi qua điểm D.4) Gọi I và K lần lượt là hình chiếu vuông góc của điểm F trên các đường thẳng CA và CB. Chứng minh rằng AB, DF, IK cùng đi qua một điểm.
Đọc tiếp
Cho ∆ABC nội tiếp đường tròn tâm O đường kính AB sao cho AC < BC; E là một điểm thuộc đoạn BC (E khác B và C). Tia AE cắt đường tròn (O) tại điểm thứ hai D. Kẻ EH vuông góc với AB tại H.
1) Chứng minh tứ giác ACEH là tứ giác nội tiếp.
2) Tia CH cắt (O) tại điểm thứ hai F. Chứng minh rằng EH // DF.
3) Chứng minh rằng đường tròn ngoại tiếp ∆CHO đi qua điểm D.
4) Gọi I và K lần lượt là hình chiếu vuông góc của điểm F trên các đường thẳng CA và CB. Chứng minh rằng AB, DF, IK cùng đi qua một điểm.
What cái gì vậy tui đăng câu hỏi cơ mà
a) Tứ giác ACEH có
ˆACE=ˆEHA=900ACE^=EHA^=900(cùng nhìn AE)
=> tứ giác ACHE nội tiếp
b) tứ giác ACHE nội tiếp
=> ˆEAH=ˆHCEEAH^=HCE^(cùng chắn EH)
lại có ˆADF=ˆACFADF^=ACF^(cùng chắn AF)
mà ˆACF+ˆHCE=900ACF^+HCE^=900do ˆACE=900ACE^=900
=>ˆEAH+ˆADF=900EAH^+ADF^=900
=> DF⊥ABDF⊥AB
mà EH⊥ABEH⊥AB
=> DF//EHDF//EH
c)các bước chứng minh nè :
cm HOD=DCH (2 góc cùng nhìn DH)
thì => COHD nọi tiếp đường tròn thì đường tròn sẽ đi qau C H O D
Cho ∆ABC nội tiếp đường tròn tâm O đường kính AB sao cho AC BC; E là một điểm thuộc đoạn BC (E khác B và C). Tia AE cắt đường tròn (O) tại điểm thứ hai D. Kẻ EH vuông góc với AB tại H.1) Chứng minh tứ giác ACEH là tứ giác nội tiếp.2) Tia CH cắt (O) tại điểm thứ hai F. Chứng minh rằng EH // DF.3) Chứng minh rằng đường tròn ngoại tiếp ∆CHO đi qua điểm D.4) Gọi I và K lần lượt là hình chiếu vuông góc của điểm F trên các đường thẳng CA và CB. Chứng minh rằng AB, DF, IK cùng đi qua một điểm.
Đọc tiếp
Cho ∆ABC nội tiếp đường tròn tâm O đường kính AB sao cho AC < BC; E là một điểm thuộc đoạn BC (E khác B và C). Tia AE cắt đường tròn (O) tại điểm thứ hai D. Kẻ EH vuông góc với AB tại H.
1) Chứng minh tứ giác ACEH là tứ giác nội tiếp.
2) Tia CH cắt (O) tại điểm thứ hai F. Chứng minh rằng EH // DF.
3) Chứng minh rằng đường tròn ngoại tiếp ∆CHO đi qua điểm D.
4) Gọi I và K lần lượt là hình chiếu vuông góc của điểm F trên các đường thẳng CA và CB. Chứng minh rằng AB, DF, IK cùng đi qua một điểm.
a) Tứ giác ACEH có
\(\widehat{ACE}=\widehat{EHA}=90^0\)(cùng nhìn AE)
=> tứ giác ACHE nội tiếp
b) tứ giác ACHE nội tiếp
=> \(\widehat{EAH}=\widehat{HCE}\)(cùng chắn EH)
lại có \(\widehat{ADF}=\widehat{ACF}\)(cùng chắn AF)
mà \(\widehat{ACF}+\widehat{HCE}=90^0\)do \(\widehat{ACE}=90^0\)
=>\(\widehat{EAH}+\widehat{ADF}=90^0\)
=> \(DF\perp AB\)
mà \(EH\perp AB\)
=> \(DF//EH\)
c)các bước chứng minh nè :
cm HOD=DCH (2 góc cùng nhìn DH)
thì => COHD nọi tiếp đường tròn thì đường tròn sẽ đi qau C H O D
Cho ∆ABC nội tiếp đường tròn tâm O đường kính AB sao cho AC BC; E là một điểm thuộc đoạn BC (E khác B và C). Tia AE cắt đường tròn (O) tại điểm thứ hai D. Kẻ EH vuông góc với AB tại H.1) Chứng minh tứ giác ACEH là tứ giác nội tiếp.2) Tia CH cắt (O) tại điểm thứ hai F. Chứng minh rằng EH // DF.3) Chứng minh rằng đường tròn ngoại tiếp ∆CHO đi qua điểm D.4) Gọi I và K lần lượt là hình chiếu vuông góc của điểm F trên các đường thẳng CA và CB. Chứng minh rằng AB, DF, IK cùng đi qua một điểm.
Đọc tiếp
Cho ∆ABC nội tiếp đường tròn tâm O đường kính AB sao cho AC < BC; E là một điểm thuộc đoạn BC (E khác B và C). Tia AE cắt đường tròn (O) tại điểm thứ hai D. Kẻ EH vuông góc với AB tại H.
1) Chứng minh tứ giác ACEH là tứ giác nội tiếp.
2) Tia CH cắt (O) tại điểm thứ hai F. Chứng minh rằng EH // DF.
3) Chứng minh rằng đường tròn ngoại tiếp ∆CHO đi qua điểm D.
4) Gọi I và K lần lượt là hình chiếu vuông góc của điểm F trên các đường thẳng CA và CB. Chứng minh rằng AB, DF, IK cùng đi qua một điểm.
cho đường tròn (O,R) hai đường kính AB và CD vuông góc với nhau . Gọi E là điểm thuộc cung nhỏ BC ( E không trùng với B,C) tiếp tuyến của đường tròn (O,R) tại E cắt đường thẳng AB tại I.Gọi F là giao điểm của DE và AB , K là điểm thuộc đường thẳng IE sao cho KF vuông góc với AB) a) chứng minh tứ giác OKEF là tứ giác nội tiếp b)chứng minh góc OKF bằng góc ODF c)chứng minh DE nhân DF bằng 2 nhân R bình phương d)Gọi M là giao điểm của OK vafCF ,tính tan góc MDC khi góc EIB bằng 45độ
Đọc tiếp
cho đường tròn (O,R) hai đường kính AB và CD vuông góc với nhau . Gọi E là điểm thuộc cung nhỏ BC ( E không trùng với B,C) tiếp tuyến của đường tròn (O,R) tại E cắt đường thẳng AB tại I.Gọi F là giao điểm của DE và AB , K là điểm thuộc đường thẳng IE sao cho KF vuông góc với AB) a) chứng minh tứ giác OKEF là tứ giác nội tiếp b)chứng minh góc OKF bằng góc ODF c)chứng minh DE nhân DF bằng 2 nhân R bình phương d)Gọi M là giao điểm của OK vafCF ,tính tan góc MDC khi góc EIB bằng 45độ
cho đường tròn O từ điểm A ngoài đường tròn vẽ đường thẳng AO cắt đường tròn O tại B , C (AB AC ) . Qua A vẽ đường thẳng không đi qua O tại D , E (ADAE). Đường thẳng vuông góc với đường thẳng CE tại F .a) Chứng minh 4 điểm A,B,E,F cùng thuộc một đường tròn b)Gọi M là giao điểm thứ hai FB với đường tròn O . Chứng minh DM vuông góc ACc) Chứng minh CE.CF+AD.AEAC^2
Đọc tiếp
cho đường tròn O từ điểm A ngoài đường tròn vẽ đường thẳng AO cắt đường tròn O tại B , C (AB <AC ) . Qua A vẽ đường thẳng không đi qua O tại D , E (AD<AE). Đường thẳng vuông góc với đường thẳng CE tại F .
a) Chứng minh 4 điểm A,B,E,F cùng thuộc một đường tròn
b)Gọi M là giao điểm thứ hai FB với đường tròn O . Chứng minh DM vuông góc AC
c) Chứng minh CE.CF+AD.AE=AC^2
Cho đường tròn tâm O đường kính AB, lấy điểm C thuộc đường tròn tâm O, với điểm C không trùng A và B. Gọi I là trung điểm của dây AC, D là giao điểm của tia OI và tiếp tuyến của đường tròn tâm O tại A. a) Chứng minh tam giác ABC vuông. b) Chứng minh DC là tiếp tuyến của đường tròn tâm O. Chứng minh DC2DI.DO c) Tia phân giác của góc BAC cắt dây BC tại điểm E và cắt đường tròn tâm O tại F, với F không trùng với A. Chứng minh rằng FA.FEFB2
Đọc tiếp
Cho đường tròn tâm O đường kính AB, lấy điểm C thuộc đường tròn tâm O, với điểm C không trùng A và B. Gọi I là trung điểm của dây AC, D là giao điểm của tia OI và tiếp tuyến của đường tròn tâm O tại A. a) Chứng minh tam giác ABC vuông. b) Chứng minh DC là tiếp tuyến của đường tròn tâm O. Chứng minh DC2=DI.DO c) Tia phân giác của góc BAC cắt dây BC tại điểm E và cắt đường tròn tâm O tại F, với F không trùng với A. Chứng minh rằng FA.FE=FB2
Cho nửa đường tròn tâm O, đường kính AB. Qua điểm C thuộc nửa đường tròn, kẻ tiếp tuyến d với đường tròn. Gọi E và F lần lượt là chân các đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ từ C đến AB. Chứng minh CE = CF












