Cho △ABC vuông tại A, trung tuyến AM. Trên tia đối của tia AM lấy điểm D sao cho MD=MA.
a) Chứng minh: △MBD=△MCA
b) Chứng minh \(\widehat{ABD}\) = 900
c) Cho AB=3 cm, BC=5 cm. Tính BD.
(Giải và vẽ hình chi tiết cho mình nha, nhất la câu b nha. Tks trước)

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD MA.a) Tính
A
B
D
^
b) Chứng minh
∆
A
B
D
∆
B
A
C
.
c) Chứng minh
A
M
1
2
B
C
Đọc tiếp
Cho tam giác ABC vuông tại A, trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Tính A B D ^
b) Chứng minh ∆ A B D = ∆ B A C .
c) Chứng minh A M = 1 2 B C
Co tam giác ABC vuông tại A Lấy đường trung tuyến Am .Trên tia đối của tia MA lấy điểm D sao cho MD=MA a) tính góc ABD b) chứng minh tam giác ABC = tam giacs BAD c) chứng minh AM =1/2 BC
Cho tam giác ABC vuông tại A, có AB = 3 cm, AC = 4 cm. Gọi AM là đường trung tuyến (M BC), trên tia đối của tia MA lấy điểm D sao cho AM = MD.
a) Tính dộ dài BC.
b) Chứng minh AB = CD, AB // CD.
c) Chứng minh góc BAM > góc CAM.
a, áp dụng định lí pytago vào tam giác ABC ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=3^2+4^2=25\)
\(BC=\sqrt{25}=5\)
B, xét tam giác BAC và DCA có:
BM=MC
AM=MD
góc BMA= DMC (đối đỉnh)
=> Tam giác BAC=DCA
=>BA=DC
Góc BAM=MDC=>BA//DC(so le trong)
cho mk xin **** nah
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có AB = 3 cm, AC = 4 cm. Gọi AM là đường trung tuyến (M BC), trên tia đối của tia MA lấy điểm D sao cho AM = MD.
a) Tính dộ dài BC.
b) Chứng minh AB = CD, AB // CD.
c) Chứng minh góc BAM > góc CAM.
Cho tam giác ABC vuông tại A, có AB = 3 cm, AC = 4 cm. Gọi AM là đường trung tuyến (M BC), trên tia đối của tia MA lấy điểm D sao cho AM = MD.
a) Tính dộ dài BC.
b) Chứng minh AB = CD, AB // CD.
c) Chứng minh góc BAM > góc CAM.
cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a. Tính số đo góc ABD.
b. Chứng minh ΔABC = ΔBAD
c. So sánh độ dài AM và BCho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a. Xét ΔAMC và ΔBMD, ta có:
BM = MC (gt)
∠(AMB) = ∠(BMC) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy (ABD) = 90o.
b. Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
c. Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.
Đúng 5
Bình luận (0)
a. Xét ΔAMC và ΔBMD, ta có:
BM = MC (gt)
∠(AMB) = ∠(BMC) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy (ABD) = 90o.
b. Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
c. Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, biết AB=6cm, AC=8cm. Kẻ đường trung tuyến AM
a/ Tính độ dài cạnh BC và AM
b/ Trên tia đối của tia MA lấy điểm D sao cho MD=MA. Chứng minh tam giác AMC= tam giác DMB.
c/ Chứng minh DB vuông AB.
Mọi người giúp mình giải nhanh nhé, vì mình đang cần gấp, cảm ơn mn.
Cho tam giác ABC vuông tại A, trung tuyến AM. Biết AB 6cm, AC 8cm.a) Trên tia đối của tia MA lấy điểm D sao cho MD MA. Chứng minh
∆
A
M
B
∆
D
M
C
.
b) Chứng minh
∆
B
A
C
∆
D
C
A
.
c) Tính AM.d) Chứng minh
A
M
A
B...
Đọc tiếp
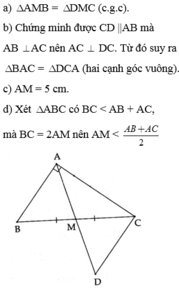
Cho tam giác ABC vuông tại A, trung tuyến AM. Biết AB = 6cm, AC = 8cm.
a) Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh ∆ A M B = ∆ D M C .
b) Chứng minh ∆ B A C = ∆ D C A .
c) Tính AM.
d) Chứng minh A M < A B + A C 2 .
Cho tam giác ABC vuông tại A (AB<AC), đường trung tuyến AM . Trên tia đối của tia MA lấy điểm N sao cho AM=MN.
a) Chứng minh: tam giác AMC=NMB. Từ đó suy ra AC=BN
b) Trên tia đối của tia BA lấy điểm D sao cho AB=BD. Gọi K là giao điểm của CD và BN. Chứng minh AK=Ck
c) Vẽ AH vuông góc B(H thuộc BC).Chứng minh : \(\widehat{MAH}=\widehat{ABC}-\widehat{ACB}\)
Hình như đề bài thiếu nha bạn