) Gọi M là trung điểm BC. Lấy điểm D sao cho O là trung điểm CD

Xét Δ BCD có M là trung điểm BC, O là trung điểm CD  OM là đường trung bình của Δ BCD

 OM=12DB và OM // DB 

mà OM⊥BC ( OM là đường trung trực của BC )  DB⊥BC

mà AH⊥BC( AH là đường cao của ΔABC )  AH // DB

Xét ΔABH và ΔBAD có

HABˆ=DBAˆ( 2 góc so le trong do AH // DB )

AB chung

ABHˆ=BADˆ( 2 góc so le trong do AH // DB )


ΔABH=ΔBAD( g-c-g )

 AH = BD mà OM=12DB  OM=12AH 

 AH = 2 OM ( đpcm )

b) Gọi G' là giao điển của AM và OH, P là trung điểm G'H, Q là trung điểm G'A

Xét Δ AG'H có P là trung điểm G'H, Q là trung điểm G'A  PQ là đường trung bình của \large\Delta AG'H 

PQ=12AH và PQ // AH

Do PQ=12AH mà OM=12AH PQ = OM

Do AH // OM ( cùng ⊥BC ) mà PQ // AH PQ // OM

Xét ΔPQG′ và ΔOMG′ có

PQG′ˆ=OMG′ˆ( 2 góc so le trong do PQ // OM)

PQ = OM (c/m trên )

QPG′ˆ=MOG′ˆ ( 2 góc so le trong do PQ //OM )


 ΔPQG′=ΔOMG′( g-c-g )

 G'Q = G'M và G'P = G'O

Ta có G'Q = G'M mà G′Q=12G′A( Q là trung điểm G'A )  G′M=12G′Amà G'M + G'A = AM 

 G′A=23AM mà AM là trung tuyến của ΔABC

 G' là trọng tâm của ΔABC ,mà G là trọng tâm của ΔABC G′≡ G

mà G′∈OH G∈OH  O, H, G thẳng hàng ( đpcm )

Hên xui nghe bạn ^ ^

Quyết Kiếm Sĩ:hên sui cái j copy trên mạng mà nổ wa :D

hình như Quyết kiếm sĩ sai rồi ấy 

dòng 9 ấy

Trọng tâm : điểm giao nhau của 3 đường trung tuyến trong Tam giác 

Trực tâm : giao giữa ba đường cao

Đường trung trực : là đường vuông góc với 1 đoạn thẳng tại trung điểm của đoạn thẳng đó.

chắc giờ trả lời là trễ lắm rồi, 2021 cơ mà. Nhưng lỡ thì kệ đi.

a) Trên tia đối của tia OC lấy điểm N sao cho ON = OC,ta có : \(OM//BN\)và \(OM=\frac{1}{2}BN\)

Vì OM \(\perp\)BC,AH \(\perp\)BC,do đó OM //AH => NB // AH

Cmtt NA/BH

Xét \(\Delta\)ANB và \(\Delta\)BHA có :

AN = AH(gt)

\(\widehat{A_1}=\widehat{A_2}\)(gt)

\(\widehat{B_1}=\widehat{B_2}\)(gt)

=> \(\Delta ANB=\Delta BHA\left(g.c.g\right)\)

=> NB = AH(hai cạnh tương ứng)

Mà \(OM=\frac{1}{2}NB\)

=> AH = 2OM

b) Gọi I là trung điểm của AG,K là trung điểm của HG thì IK//AH => IK//OM,do đó \(\widehat{KIG}=\widehat{OMG}\)(so le trong)

Xét \(\Delta KGI\)và \(\Delta OMG\)có :

GI = GM(gt)

\(\widehat{G_1}=\widehat{G_2}\)(đối đỉnh)

\(\widehat{I}=\widehat{M}\)

=> \(\Delta KGI=\Delta OGM\left(g.c.g\right)\)

=> KG = GO

Từ đó ta có : HG = GO.

Hình vẽ :

Chứng minh:
Các điểm được đặt tên như hình vẽ: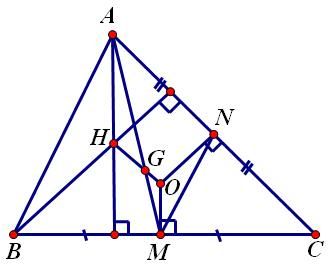

Ta có: 

Cơ mà 
Lại có: 

Nguồn: Mạng

Chỉ chứng minh được câu b thui

lop 6 sao ma lam duoc

bn vẽ hình giùm mk đi, hoặc giải thích thế nào là trực tâm, trọng tâm z?

mik cũng ko bít trực tâm, trọng tâm là j. 

Muốn gải thì phải tự kẻ hình, chứ người ta lười vẽ lắm

a,+) Lấy N sao cho : O là trung điểm của CN ; lấy M sao cho : OM là trung trực của BC

\(\implies\) OM là đường trung bình của tam giác CNB 

\(\implies\) OM song song với NB ; OM = \(\frac{1}{2}\) NB 

Ta có : OM vuông góc với BC \(\implies\) NB vuông góc với BC mà AH vuông góc với BC

\(\implies\) NB song song với AH ( 1 )

+) Lấy S sao cho : OS là trung trực của AC ; mà O là trung điểm của NC 

\(\implies\) OS là đường trung bình của tam giác NAC

\(\implies\) OS song song với AN ; OS = \(\frac{1}{2}\) AN

Ta có : OS vuông góc với AC \(\implies\) NA vuông góc với AC mà BH vuông góc với AC 

\(\implies\) NA song song với BH ( 2 )

Từ ( 1 ) ; ( 2 )

 \(\implies\) NAHB là hình bình hành 

 \(\implies\) NB = AH ( 3 )

Mà OM = \(\frac{1}{2}\) NB \(\implies\) 2OM = NB ( 4 )

Từ ( 3 ) ; ( 4 ) 

\(\implies\) AH = 2OM ( đpcm )

b, Ta có : A ; G ; M thẳng hàng ( M là trung điểm của BC ; G là trọng tâm )

 GM = \(\frac{1}{3}\) AM \(\implies\) AG = 2GM 

 Gọi I ; K lần lượt là trung điểm của HG ; AG 

\(\implies\) IK là đường trung bình của tam giác HGA 

\(\implies\) IK song song với AH ; IK = \(\frac{1}{2}\) AH

+) NB song song OM , mà NB song song với AH 

\(\implies\) AH song song với OM 

+) AH song song với OM , mà IK song song với AH 

\(\implies\) IK song song với OM

\(\implies\) IKG = GMO ( 2 góc so le trong )

+) IK = \(\frac{1}{2}\) AH , mà AH = 2OM

\(\implies\) IK = OM 

+) K là trung điểm của AG

\(\implies\) KA = KG = \(\frac{AG}{2}\)

Mà AG = 2GM \(\implies\) KA = KG = GM \(\implies\) KG = GM

+)Xét tam giác KIG và tam giác MOG có :

 KG = GM 

 IKG = GMO ( cmt )

 OM = KI 

\(\implies\) tam giác KIG = tam giác MOG ( c - g - c )

\(\implies\) IGK = OGM ( 2 góc tương ứng )

Mà 2 góc này ở vị trí 2 góc đối đỉnh 

\(\implies\) I , G , O thẳng hàng

\(\implies\) H , G , O thẳng hàng 

+) I là trung điểm của HG 

\(\implies\) IH = IG = \(\frac{HG}{2}\)

\(\implies\) 2IH = 2IG = HG ( 5 )

+) IG = GO ( tam giác KIG = tam giác MOG )

​​​\(\implies\)​ 2IG = 2GO ( 6 )

Từ ( 5 ) ; ( 6 ) 

\(\implies\) HG = 2GO

Trong một tam giác :

+)3 đường trung tuyến đồng quy : trọng tâm

+)3 đường phân giác đồng quy : tâm đường tròn nội tiếp tam giác

+)3 đường cao đồng quy : trực tâm

+)3 đường trung trực đồng quy : tâm đường tròn ngoại tiếp tam giác