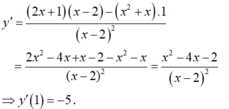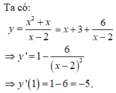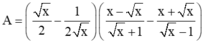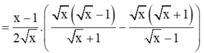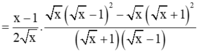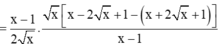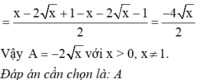P(x)= x199+ xx198 +... + x2 + xx tại x= -1

Những câu hỏi liên quan
G = (x+1x−1+xx+1+x1−x2):(x+1x−1+1−xx+1)(x+1x−1+xx+1+x1−x2):(x+1x−1+1−xx+1)
a) Rút gọn G b) Tìm giá trị nhỏ nhất của G với x > 0
c) Tính G tại | x - 3 | = 2 d) Tìm x với G = 1 ; G < 0
Cho hàm số y = x 2 + x x - 2 đạo hàm của hàm số tại x = 1 là:
A. y'(1)= -4
B. y'(1)= -5
C. y'(1)= -3
D. y'(1)= -2
Cho hàm số y = x 2 + x x - 2 , đạo hàm của hàm số tại x= 1 là:
A. y'(1)= -4
B.y'(1)= -3
C.y'(1)= -2
D.y'(1)= -5
Cho hàm số
y
x
2
+
x
x
-
2
đạo hàm của hàm số tại x 1 là: A. - 4 B. - 5 C. - 3 D. -2
Đọc tiếp
Cho hàm số y = x 2 + x x - 2 đạo hàm của hàm số tại x= 1 là:
A. - 4
B. - 5
C. - 3
D. -2
Chọn B.
y ' = ( 2 x + 1 ) . ( x − 2 ) − 1. ( x 2 + x ) ( x − 2 ) 2 = x 2 − 4 x − 2 ( x − 2 ) 2
y ' ( 1 ) = 1 2 − 4.1 − 2 ( 1 − 2 ) 2 = − 5
Đúng 0
Bình luận (0)
Rút gọn biểu thức
A
x
2
-
1
2
x
x
-
x
x
+
1
-
x...
Đọc tiếp
Rút gọn biểu thức A = x 2 - 1 2 x x - x x + 1 - x + x x - 1 với x > 0, x ≠ 1.
A. A = –2 x
B. A = 2 x
C. A = – x
D. A = 4 x
rút gọn:
1. 2√3−6√8−223−68−2
2. x2+√xx−√x+1−2x+√x√xx2+xx−x+1−2x+xx
3. x√x−1−2x−√xx−√x
Tính:19 x 29 x 39 x....x199 kết quả có chữ số tận cùng là:
phép tính có số thừa số là: (199-19):10+1=19 thừa số
Ta thấy: nếu 2 số tận cùng là 9 nhân với nhau sẽ tận cùng là 1, 3 số tận cùng là 9
=> lẻ chữ số tận cùng là 9 nhân với nhau sẽ tận cùng là 9
Đúng 0
Bình luận (0)
Chữ số tận cùng là 9
Ai thấy đúng thì tk cho mk nha!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình bằng cách đặt ẩn phụ:
a
)
3.
x
2
+
x
2
−
2
x
2
+
x...
Đọc tiếp
Giải phương trình bằng cách đặt ẩn phụ:
a ) 3. x 2 + x 2 − 2 x 2 + x − 1 = 0 b ) x 2 − 4 x + 2 2 + x 2 − 4 x − 4 = 0 c ) x − x = 5 x + 7 d ) x x + 1 − 10 ⋅ x + 1 x = 3
a)
3 · x 2 + x 2 - 2 x 2 + x - 1 = 0 ( 1 )
Đặt t = x 2 + x ,
Khi đó (1) trở thành : 3 t 2 – 2 t – 1 = 0 ( 2 )
Giải (2) : Có a = 3 ; b = -2 ; c = -1
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 ; t 2 = c / a = - 1 / 3 .
+ Với t = 1 ⇒ x 2 + x = 1 ⇔ x 2 + x – 1 = 0 ( * )
Có a = 1; b = 1; c = -1 ⇒ Δ = 1 2 – 4 . 1 . ( - 1 ) = 5 > 0
(*) có hai nghiệm
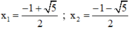
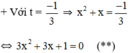
Có a = 3; b = 3; c = 1 ⇒ Δ = 3 2 – 4 . 3 . 1 = - 3 < 0
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm 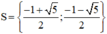
b)
x 2 − 4 x + 2 2 + x 2 − 4 x − 4 = 0 ⇔ x 2 − 4 x + 2 2 + x 2 − 4 x + 2 − 6 = 0 ( 1 )
Đặt x 2 – 4 x + 2 = t ,
Khi đó (1) trở thành: t 2 + t – 6 = 0 ( 2 )
Giải (2): Có a = 1; b = 1; c = -6
⇒ Δ = 1 2 – 4 . 1 . ( - 6 ) = 25 > 0
⇒ (2) có hai nghiệm
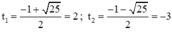
+ Với t = 2 ⇒ x 2 – 4 x + 2 = 2
⇔ x 2 – 4 x = 0
⇔ x(x – 4) = 0
⇔ x = 0 hoặc x = 4.
+ Với t = -3 ⇒ x 2 – 4 x + 2 = - 3
⇔ x2 – 4x + 5 = 0 (*)
Có a = 1; b = -4; c = 5 ⇒ Δ ’ = ( - 2 ) 2 – 1 . 5 = - 1 < 0
⇒ (*) vô nghiệm.
Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.
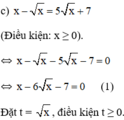
Khi đó (1) trở thành: t 2 – 6 t – 7 = 0 ( 2 )
Giải (2): Có a = 1; b = -6; c = -7
⇒ a – b + c = 0
⇒ (2) có nghiệm t 1 = - 1 ; t 2 = - c / a = 7 .
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
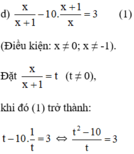
⇔ t 2 – 10 = 3 t ⇔ t 2 – 3 t – 10 = 0 ( 2 )
Giải (2): Có a = 1; b = -3; c = -10
⇒ Δ = ( - 3 ) 2 - 4 . 1 . ( - 10 ) = 49 > 0
⇒ (2) có hai nghiệm:
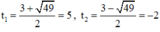
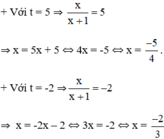
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có tập nghiệm 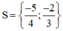
Đúng 0
Bình luận (0)
Rút gọn biểu thức:
P
x
−
x
+
2
x
−
x
−
2
−
x
x
−...
Đọc tiếp
Rút gọn biểu thức: P = x − x + 2 x − x − 2 − x x − 2 x : 1 − x 2 − x với x > 0 ; x ≠ 1 ; x ≠ 4
Ta có: P = x − x + 2 ( x + 1 ) ( x − 2 ) − x x ( x − 2 ) : 1 − x 2 − x = x − x + 2 − x ( x + 1 ) ( x + 1 ) ( x − 2 ) . 2 − x 1 − x = 2 − 2 x ( x + 1 ) ( x − 1 ) = 2 ( 1 − x ) ( x + 1 ) ( x − 1 ) = − 2 x + 1
Đúng 0
Bình luận (0)
Hàm số nào dưới đây không là nguyên hàm của hàm số sau ?
f
x
x
x
+
2
x
+
1
2...
Đọc tiếp
Hàm số nào dưới đây không là nguyên hàm của hàm số sau ? f x = x x + 2 x + 1 2
A. x 2 + x - 1 x + 1 B. x 2 - x - 1 x + 1
C. x 2 + x + 1 x + 1 D. x 2 x + 1
Đáp án: A.
Hướng dẫn: Ta có B, C và D. Chỉ kiểm tra D đúng, còn B và C sai khác với D hằng số -1, 1.
Đúng 0
Bình luận (0)