`C4:`

`x/[x-2]+2/[2-x]=x/[x-2]-2/[x-2]=[x-2]/[x-2]=1`

`C5:[15x^2]/[17y^4] . [34y^5]/[15x^3]`

 `=[15x^2 . 2.17y^4 . y]/[17y^4 . 15x^2 . x]=[2y]/x`

`C5:[6x+18]/[(x+4)^2]:[3(x+3)]/[x+4]`

 `=[6(x+3)]/[(x+4)^2] . [x+4]/[3(x+3)]`

`=2/[x+4]`

\(\left(3x+2\right)\left(3x-2\right)=9x^2-4\)

-> chọn D 

Điều kiện xác định là

Ta có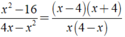 

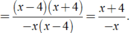
Chọn đáp án C.

a, ĐKXĐ :\(x\ne3;x\ne-3\)

b, \(P=\frac{3\cdot\left(x-3\right)}{\left(x-3\right)\cdot\left(x+3\right)}+\frac{x+3}{\left(x+3\right)\cdot\left(x-3\right)}+\frac{18}{\left(x+3\right)\cdot\left(x-3\right)}\)

       \(=\frac{3x-9+x+3+18}{\left(x+3\right)\cdot\left(x-3\right)}\)\(=\frac{4x+12}{\left(x-3\right)\cdot\left(x+3\right)}\)

        \(=\frac{4\cdot\left(x+3\right)}{\left(x+3\right)\cdot\left(x-3\right)}=\frac{4}{x-3}\)

c, Với P = 4 \(\Rightarrow\frac{4}{x-3}=4\Rightarrow4=4\cdot\left(x-3\right)\)\(\Rightarrow1=x-3\Rightarrow x=4\)

a) đk: \(\hept{\begin{cases}a\ge0\\a\ne16\end{cases}}\)

Ta có: 

\(C=\frac{a}{a-16}-\frac{2}{\sqrt{a}-4}-\frac{2}{\sqrt{a}+4}\)

\(C=\frac{a-2\cdot\left(\sqrt{a}+4\right)-2\cdot\left(\sqrt{a}-4\right)}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}\)

\(C=\frac{a-2\sqrt{a}-8-2\sqrt{a}+8}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}\)

\(C=\frac{a-4\sqrt{a}}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}=\frac{\sqrt{a}}{\sqrt{a}+4}\)

b) Ta có: \(a=9-4\sqrt{5}=\left(\sqrt{5}-2\right)^2\)

\(\Rightarrow\sqrt{a}=\sqrt{5}-2\)

Khi đó: \(C=\frac{\sqrt{5}-2}{\sqrt{5}-2+4}=\frac{\sqrt{5}-2}{\sqrt{5}+2}=\frac{\left(\sqrt{5}-2\right)^2}{1}=9-4\sqrt{5}\)

\(C=\frac{a}{a-16}-\frac{2}{\sqrt{a}-4}-\frac{2}{\sqrt{a}+4}\)

a) ĐKXĐ : \(\hept{\begin{cases}a\ge0\\a\ne16\end{cases}}\)

\(=\frac{a}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}-\frac{2\left(\sqrt{a}+4\right)}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}-\frac{2\left(\sqrt{a}-4\right)}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}\)

\(=\frac{a-2\sqrt{a}-8-2\sqrt{a}+8}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}\)

\(=\frac{a-4\sqrt{a}}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}\)

\(=\frac{\sqrt{a}\left(\sqrt{a}-4\right)}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}=\frac{\sqrt{a}}{\sqrt{a}+4}\)

b) Với \(a=9-4\sqrt{5}\)( tmđk )

\(C=\frac{\sqrt{a}}{\sqrt{a}+4}=1-\frac{4}{\sqrt{a}+4}\)

\(C=1-\frac{4}{\sqrt{9-4\sqrt{5}}+4}\)

\(=1-\frac{4}{\sqrt{5-4\sqrt{5}+4}+4}\)

\(=1-\frac{4}{\sqrt{\left(\sqrt{5}-2\right)^2}+4}\)

\(=1-\frac{4}{\left|\sqrt{5}-2\right|+4}\)

\(=1-\frac{4}{\sqrt{5}-2+4}\)

\(=1-\frac{4}{\sqrt{5}+2}\)

\(=\frac{\sqrt{5}+2-4}{\sqrt{5}+2}\)

\(=\frac{\sqrt{5}-2}{\sqrt{5}+2}\)

\(=\frac{\left(\sqrt{5}-2\right)\left(\sqrt{5}-2\right)}{1}=9-4\sqrt{5}\)

Chọn B