Cho tam giác ABC có ha=3, hb=4, hc=6. Tính r
Những câu hỏi liên quan
cho tam giác ABC có các đường phân giác cắt nhau tại N cho ha, hb,hc là đường cao gọi r là khoảng cách từ N đến cạnh tam giác. chứng minh rằng 1/ha+1/hb+1/hc=1/r
2S(ABC)=ha.a=hb.b=hc.c suy ra 1/ha+1/hb+1/hc=a/2S+b/2S+c/2S=1/2S .(a+b+c)=1/r(a+b+c) .(a+b+c) =1/r (đpcm) (vì 2S=r(a+b+c))
Đúng 0
Bình luận (1)
Tam giác ABC có
A
^
100
0
và trực tâm H. Tính tổng
H
A
→
,
H
B
→
+
H
B
→...
Đọc tiếp
Tam giác ABC có A ^ = 100 0 và trực tâm H. Tính tổng H A → , H B → + H B → , H C → + H C → , H A → .
A. 360 °
B. 180 °
C. 80 °
D. 160 °
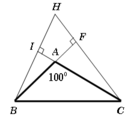
Vì H I A ^ + H F A ^ = 180 0 nên tứ giác HFAI nội tiếp.
Suy ra: I H F ^ + I A F ^ = 180 0 ⇒ I H F ^ = 180 0 − I A F ^ = 80 0
Ta có H A → , H B → = B H A ^ H B → , H C → = B H C ^ H C → , H A → = C H A ^
⇒ H A → , H B → + H B → , H C → + H C → , H A → = B H A ^ + B H C ^ + C H A ^
= 2 B H C ^ = 2.80 0 = 160 0
Chọn D.
Đúng 0
Bình luận (0)
Cho tam giác ABC có chu vi 2p ngoại tiếp (I;r). Gọi a,b,c; ha,hb,hc thứ tự là độ dài và chiều cao tương ứng cạnh BC,CA,AB. Chứng minh:
a) 1/ha + 1/hb + 1/hc = 1/r
b) ha + hb + hc =2pr( 1/a + 1/b + 1/c )
Cho tam giác ABC có chu vi 2p ngoại tiếp (I;r). Gọi a,b,c; ha,hb,hc thứ tự là độ dài và chiều cao tương ứng cạnh BC,CA,AB. Chứng minh:
a) 1/ha + 1/hb + 1/hc = 1/r
b) ha + hb + hc =2pr( 1/a + 1/b + 1/c )
Cho tam giác ABC với BC = a, CA = b, AB = c và ba đường cao ứng với ba cạnh lần lượt có độ dài ha,hb,hc Gọi r là khoảng cách từ giao điểm của ba đường phân giác của tam giác đến một cạnh của tam giác. Chứng minh 1/ha+1/hb+1/hc=1/r
Cho tam giác ABC có trực tâm H. Biểu thức
A
H
→
.
H
B
→
−
H
C
→
+
B
H
→
.
H...
Đọc tiếp
Cho tam giác ABC có trực tâm H.
Biểu thức A H → . H B → − H C → + B H → . H C → − H A → + C H → . H A → − H B → bằng
A. 0 →
B.0
C. A B 2 + B C 2 + C A 2
D. 1 2 A B 2 + B C 2 + C A 2
Vì H là trực tâm tam giác ABC nên:
A H ⊥ C B ; B H ⊥ A C ; C H ⊥ B A ⇒ A H → . C B → = 0 ; B H → . A C → = 0 ; C H → . B A → = 0
Ta có
A H → . H B → − H C → + B H → . H C → − H A → + C H → . H A → − H B →
= A H → . C B → + B H → . A C → + C H → . B A → = 0
CHỌN B
Đúng 0
Bình luận (0)
Cho tam giác ABC có tâm đường tròn ngoại tiếp O. Tính
H
A
→
+
H
B
⇀
+
H
C
⇀
A.
2
H
O
→
B.
H...
Đọc tiếp
Cho tam giác ABC có tâm đường tròn ngoại tiếp O. Tính H A → + H B ⇀ + H C ⇀
A. 2 H O →
B. H O →
C. A C →
D. Tất cả sai
Cho tam giác ABC , AB =c , BC=a , CA =b và vẽ đường cao tường ứng với 3 cạnh là hc , hb , ha . Gọi r là khoảng cách từ giao điểm 3 đường phân giác đến 3 cạnh tam giác
Chứng minh \(\frac{1}{ha}+\frac{1}{hb}+\frac{1}{hc}=\frac{1}{r}\)