chứng minh rằng các cặp phân số sau đây = nhau :
a, ab/abab= 3/303
b, 7x-21/14x-42=2/4
Dùng tính chất cơ bản của phân số, giải thích tại sao các phân số sau đây bằng nhau:
a)-28/21=52/-39
b)18180/-27270/2/-3
d)ab/cd=ab0ab/cd0cd
7x-21/14x-42=1/2
a) Ta có: \(\frac{-28}{21}=\frac{-4}{3}\)
\(\frac{52}{-39}=\frac{-4}{3}\)
\(\Rightarrow\frac{-28}{21}=\frac{52}{-39}\left(đpcm\right)\)Bài này rút gọn là ra nhé!
b) Đề này phải ko: \(\frac{18180}{-27270}=\frac{-2}{3}\)
Ta có: \(\frac{18180}{-27270}=-\frac{2}{3}\left(đpcm\right)\)Bài này cx rút gọn nhé!
d)???
Bài 2 : Hãy chứng minh rằng :
a) ab / abab = 3/303
b) 7x - 21/ 14x - 42 = 2/4
c) 9x - 18 / 18y - 54 = 2x - 4 / 4y - 12
d) xy - x2 / y2 - xy = x / y
Cho hai số nguyên a và b (b ≠ 0). Chứng minh rằng các cặp phân số sau đây luôn bằng nhau:
- a - b v à a b
Ta có: (-a) . b = - (a . b) = a . (-b).
Do đó 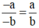 (theo định nghĩa SGK).
(theo định nghĩa SGK).
Cho hai số nguyên a và b (b ≠ 0). Chứng minh rằng các cặp phân số sau đây luôn bằng nhau:
a - b v à - a b
Ta có (-a) . (-b) = a . b
Do đó 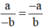 (theo định nghĩa SGK).
(theo định nghĩa SGK).
Cho hai số nguyên a và b (b ≠ 0). Chứng minh rằng các cặp phân số sau đây luôn bằng nhau:
- a - b v à a b
Ta có: (-a) . b = - (a . b) = a . (-b).
Do đó 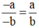 (theo định nghĩa SGK).
(theo định nghĩa SGK).
Cho hai số nguyên a và b (b ≠ 0). Chứng minh rằng các cặp phân số sau đây luôn bằng nhau:
a - b v à - a b
Ta có (-a) . (-b) = a . b
Do đó 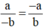 (theo định nghĩa SGK).
(theo định nghĩa SGK).
\(\frac{7x-21}{14x-42}\)=\(\frac{1}{2}\)giải thích vì sao các phân số bằng nhau
ĐK : x \(\ne\)3
\(\frac{7x-21}{14x-42}=\frac{1}{2}\Leftrightarrow14x-42=14x-42\)
\(\Leftrightarrow0=0\)*đúng* | Vậy vô nghiệm, mk chưa hc nên cx ko biết KL
\(\frac{7x-21}{14x-42}=\frac{7x-21}{2\left(7x-21\right)}=\frac{1}{2}=VP\)( ddpcm )
Giair thích à, xin lỗi chưa đọc đề :
Thế KL là ta có đpcm nhé
Cho hai số nguyên a, b (b khác 0). Chứng tỏ rằng các cặp phân số sau đây luôn bằng nhau:
a) a − b = − a b
b) − a − b = a b
a) a − b = a . ( − 1 ) − b . ( − 1 ) = − a b
b) − a − b = − a . ( − 1 ) − b . ( − 1 ) = a b
Giải thích tại sao các phân số sau đây bằng nhau:
a) a b = − a − b
b) a b a b ¯ c d c d ¯ = a b a b a b ¯ c d c d c d ¯
c) a b a b ¯ a b a b a b ¯ = 101 10101
a) a b = a . ( − 1 ) b . ( − 1 ) = − a − b
b) ta có:
a b a b ¯ c d c d ¯ = a b a b ¯ : 101 c d c d ¯ : 101 = a b ¯ c d ¯ ; a b a b a b ¯ c d c d ¯ c d = a b a b a b ¯ : 10101 c d c d ¯ c d:10101 = a b ¯ c d ¯
do đó: a b a b ¯ c d c d ¯ = a b a b a b ¯ c d c d ¯ c d
c) a b a b ¯ a b a b a b ¯ = a b a b ¯ : a b ¯ a b a b a b ¯ : a b ¯ = 101 10101