Cho 2 đường tròn (O),(O') cắt nhau tại A,B.Dây AC của (O') tiếp xúc với (O) tại A.Gọi K là điểm đối xứng với A qua trung điểm I của OO'.E đối xứng với A qua B Chứng minh A,C,E,D thuộc 1 đường tròn

Những câu hỏi liên quan
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A. Dây AD của đường trong (O’) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO’, E là điểm đối xứng với A qua B. Chứng minh rằng: Bốn điểm A, C, E, D cùng nằm trên một đường tròn
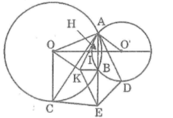
Vì AB ⊥ KB nên AE ⊥ KB
Lại có: AB = BE (tính chất đối xứng tâm)
Suy ra: KA = KE (tính chất đường trung trực) (3)
Ta có: IO = IO’ (gt)
IA = IK (chứng minh trên)
Tứ giác AOKO’ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: OK // O’A và OA // O’K
CA ⊥ O’A (vì CA là tiếp tuyến của đường tròn (O’))
OK // O’A (chứng minh trên)
Suy ra: OK ⊥ AC
Khi đó OK là đường trung trực của AC
Suy ra: KA = KC (tính chất đường trung trực) (4)
DA ⊥ OA (vì DA là tiếp tuyến của đường tròn (O))
O’K // OA (chứng minh trên)
Suy ra: O’K ⊥ DA
Khi đó O’K là đường trung trực của AD
Suy ra: KA = KD (tính chất đường trung trực) (5)
Từ (3), (4) và (5) suy ra: KA = KC = KE = KD
Vậy bốn điểm A, C, E, D cùng nằm trên một đường tròn.3
Đúng 0
Bình luận (0)
cho hai đường tròn (O) và (O') cắt nhau tại A và B .Dây AC của đường tròn (O) tiếp xúc với đường tròn (O') tại A.Dây AD của đường tròn (O') tiếp xúc với đường tròn (O) tại A.Gọi K là điểm đối xứng với A qua trung điểm I của OO' ,E là điểm đối xứng với A và B.cmr:
a)AB vuông góc với KB
b)Bốn điểm A,C,E,D nằm trên cùng một đường tròn
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A. Dây AD của đường trong (O’) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO’, E là điểm đối xứng với A qua B. Chứng minh rằng: AB ⊥ KB
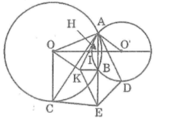
Gọi H là giao điểm của AB và OO’
Vì OO’ là đường trung trực của AB nên OO’ ⊥ AB tại H
Ta có: HA = HB
I là trung điểm của OO’ nên IH ⊥ AB (1)
Trong tam giác ABK, ta có:
HA = HB (chứng minh trên)
IA = IK (tính chất đối xứng tâm)
Suy ra IH là đường trung bình của tam giác ABK
Suy ra IH // BK (2)
Từ (1) và (2) suy ra: AB ⊥ KB
Đúng 0
Bình luận (0)
Cho 2 đường tròn tâm O và O cắt nhau tại A và B dây AC của (O) tiếp xúc với (O ) tại A. Dây AD của (O ) tiếp xúc với (O) tại A Gọi K là điểm đối xứng với A qua trung điểm I của OO . E là điểm đối xứng với A qua B. Chứng minh rằng:
a) AB vuông góc với KB
b) 4 điểm A;C;D;E nằm trên một đường tròn
Cho 2 đường tròn tâm O và O cắt nhau tại A và B dây AC của (O) tiếp xúc với (O ) tại A. Dây AD của (O ) tiếp xúc với (O) tại A Gọi K là điểm đối xứng với A qua trung điểm I của OO . E là điểm đối xứng với A qua B. Chứng minh rằng:
a) AB vuông góc với KB
b) 4 điểm A;C;D;E nằm trên một đường tròn
Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O) tại A. Dây AD của đường tròn (O) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO, E là điểm đối xứng với A qua B. Chứng minh rằng :
a) ABperp KB
b) Bốn điểm A, C, E, D nằm trên cùng một đường tròn
Đọc tiếp
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O') tại A. Dây AD của đường tròn (O') tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO', E là điểm đối xứng với A qua B. Chứng minh rằng :
a) \(AB\perp KB\)
b) Bốn điểm A, C, E, D nằm trên cùng một đường tròn
cho hai đường tròn (O) và (O') cắt nhau tại A và B.Trên (O) và (O') lần luọt lấy C và D sao cho AC, AD là tiếp tuyến của (O), (O'). Gọi E là điểm đối xứng với A qua trung điểm I của đoạn thẳng OO' và G là điểm đối xứng với A qua B. CMR: A, C, G, D cùng thuộc một đường tròn
Cho tam giác ABC vuông tại A và điểm M thuộc cạnh AC. Vẽ đường tròn tâm O đường kính MC cắt BC tại E. Nối BM cắt đường tròn (O) tại N, AN cắt đường tròn (O) tại D. Lấy I đối xứng với M qua A, K đối xứng với M qua Ea, Chứng minh BANC là tứ giác nội tiếpb, Chứng minh CA là phân giác của
B
C
D
^
c, Chứng minh ABED là hình thangd, Tìm vị trí M để đường tròn ngoại tiếp tam giác BIK có...
Đọc tiếp
Cho tam giác ABC vuông tại A và điểm M thuộc cạnh AC. Vẽ đường tròn tâm O đường kính MC cắt BC tại E. Nối BM cắt đường tròn (O) tại N, AN cắt đường tròn (O) tại D. Lấy I đối xứng với M qua A, K đối xứng với M qua E
a, Chứng minh BANC là tứ giác nội tiếp
b, Chứng minh CA là phân giác của B C D ^
c, Chứng minh ABED là hình thang
d, Tìm vị trí M để đường tròn ngoại tiếp tam giác BIK có bán kính nhỏ nhất
a, Học sinh tự chứng minh
b, Học sinh tự chứng minh
c, Học sinh tự chứng minh
d, Chú ý: B I A ^ = B M A ^ , B M C ^ = B K C ^
=> Tứ giác BICK nội tiếp đường tròn (T), mà (T) cũng là đường tròn ngoại tiếp DBIK. Trong (T), dây BC không đổi mà đường kính của (T) ≥ BC nên đường kính nhỏ nhất bằng BC
Dấu "=" xảy ra <=> B I C ^ = 90 0 => I ≡ A => MA
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính AB.Trên tia tiếp tuyến của (O) tại A,lấy điểm M khác A. Đường thẳng MB cắt đường tròn (O) tại C. Qua A kẻ đường thẳngvuông góc với OM tại I, đường thẳng này cắt đường tròn (O) tại D.a) Chứng minh MD là tiếp tuyến của (O)b) Chứng minh ∆MAC vuông tại C .c) Chứng minh rằng MCDMDBd) Tiếp tuyến với đường tròn ngoại tiếp ∆AMD tại điểm A cắt (O) ở P. E là điểmđối xứng với A qua D. Chứng minh rằng bốn điểm A, M, E, P cùng thuộc mộtđường tròn.
Đọc tiếp
Cho đường tròn (O) đường kính AB.Trên tia tiếp tuyến của (O) tại A,
lấy điểm M khác A. Đường thẳng MB cắt đường tròn (O) tại C. Qua A kẻ đường thẳng
vuông góc với OM tại I, đường thẳng này cắt đường tròn (O) tại D.
a) Chứng minh MD là tiếp tuyến của (O)
b) Chứng minh ∆MAC vuông tại C .
c) Chứng minh rằng MCD=MDB
d) Tiếp tuyến với đường tròn ngoại tiếp ∆AMD tại điểm A cắt (O) ở P. E là điểm
đối xứng với A qua D. Chứng minh rằng bốn điểm A, M, E, P cùng thuộc một
đường tròn.
haha em không biết câu trả lời em mới học lớp 6












