giải các phương trình
a) ( x - 7 )(2x + 5 ) = 0
b) 4x2- 6x = 0
Những câu hỏi liên quan
Giải các phương trình sau:a)
7
−
x
2
4
−
x
+
5
2
0
;
b)
4
x
2
+
x
−
1...
Đọc tiếp
Giải các phương trình sau:
a) 7 − x 2 4 − x + 5 2 = 0 ;
b) 4 x 2 + x − 1 2 − 2 x + 1 2 = 0 ;
c) x 3 + 1 = x + 1 2 − x ;
d) x 2 − 4 x − 5 = 0 .
Giải các phương trình sau:a)
x
−
1
2
−
2
x
+
5
2
0
;
b)
x
2
−
1
−
x
2...
Đọc tiếp
Giải các phương trình sau:
a) x − 1 2 − 2 x + 5 2 = 0 ;
b) x 2 − 1 − x 2 − 2 x − 1 2 = 0 ;
c) x 3 + 8 = − 2 x x + 2 ;
d) 4 x 2 + 8 x − 5 = 0 .
Giải các phương trình sau:a)
2
x
−
1
2
+
x
−
3
2
x
−
1
0
;
b)
3
−
2
x...
Đọc tiếp
Giải các phương trình sau:
a) 2 x − 1 2 + x − 3 2 x − 1 = 0 ;
b) 3 − 2 x 2 + 4 x 2 − 9 = 0 ;
c) 7 − x 2 + 2 3 x − 7 x − 3 = 0 ;
d) 4 3 x − 2 − 3 x − 2 3 = 0 .
Giải các phương trình sau: 4 x 2 - 3 x + 2 - 3 x 2 - 6 x + 5 = 0
Giải các phương trình sau:a)
9
−
x
2
x
;
b)
x
−
15
+
1
3
x
;
c)
4
x
2
−
1
+
3
x...
Đọc tiếp
Giải các phương trình sau:
a) 9 − x = 2 x ; b) x − 15 + 1 = 3 x ;
c) 4 x 2 − 1 + 3 x 2 x − 1 = 0 ; d) 5 − 4 x = 4 − 5 x .
Giải các phương trình tích sau:1.a)(3x – 2)(4x + 5) 0 b) (2,3x – 6,9)(0,1x + 2) 0c)(4x + 2)(x2 + 1) 0 d) (2x + 7)(x – 5)(5x + 1) 02. a)(3x + 2)(x2 – 1) (9x2 – 4)(x + 1) b)x(x + 3)(x – 3) – (x + 2)(x2 – 2x + 4) 0c)2x(x – 3) + 5(x – 3) 0 d)(3x – 1)(x2 + 2) (3x – 1)(7x – 10)3.a)(2x – 5)2 – (x + 2)2 0 b)(3x2 + 10x – 8)2 (5x2 – 2x + 10)2c)(x2 – 2x + 1) – 4 0 d)4x2 + 4x + 1 x24. a) 3x2 + 2x – 1 0 b) x2 – 5x + 6 0c) x2 – 3x + 2 0 d) 2x2 – 6x + 1 0 ...
Đọc tiếp
Giải các phương trình tích sau:
1.a)(3x – 2)(4x + 5) = 0 b) (2,3x – 6,9)(0,1x + 2) = 0
c)(4x + 2)(x2 + 1) = 0 d) (2x + 7)(x – 5)(5x + 1) = 0
2. a)(3x + 2)(x2 – 1) = (9x2 – 4)(x + 1)
b)x(x + 3)(x – 3) – (x + 2)(x2 – 2x + 4) = 0
c)2x(x – 3) + 5(x – 3) = 0 d)(3x – 1)(x2 + 2) = (3x – 1)(7x – 10)
3.a)(2x – 5)2 – (x + 2)2 = 0 b)(3x2 + 10x – 8)2 = (5x2 – 2x + 10)2
c)(x2 – 2x + 1) – 4 = 0 d)4x2 + 4x + 1 = x2
4. a) 3x2 + 2x – 1 = 0 b) x2 – 5x + 6 = 0
c) x2 – 3x + 2 = 0 d) 2x2 – 6x + 1 = 0
e) 4x2 – 12x + 5 = 0 f) 2x2 + 5x + 3 = 0
Bài 1:
a) (3x - 2)(4x + 5) = 0
<=> 3x - 2 = 0 hoặc 4x + 5 = 0
<=> 3x = 2 hoặc 4x = -5
<=> x = 2/3 hoặc x = -5/4
b) (2,3x - 6,9)(0,1x + 2) = 0
<=> 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0
<=> 2,3x = 6,9 hoặc 0,1x = -2
<=> x = 3 hoặc x = -20
c) (4x + 2)(x^2 + 1) = 0
<=> 4x + 2 = 0 hoặc x^2 + 1 # 0
<=> 4x = -2
<=> x = -2/4 = -1/2
d) (2x + 7)(x - 5)(5x + 1) = 0
<=> 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0
<=> 2x = -7 hoặc x = 5 hoặc 5x = -1
<=> x = -7/2 hoặc x = 5 hoặc x = -1/5
bài 2:
a, (3x+2)(x^2-1)=(9x^2-4)(x+1)
(3x+2)(x-1)(x+1)=(3x-2)(3x+2)(x+1)
(3x+2)(x-1)(x+1)-(3x-2)(3x+2)(x+1)=0
(3x+2)(x+1)(1-2x)=0
b, x(x+3)(x-3)-(x-2)(x^2-2x+4)=0
x(x^2-9)-(x^3+8)=0
x^3-9x-x^3-8=0
-9x-8=0
tự tìm x nha
Đúng 0
Bình luận (0)
Giải các phương trình:
b) x 2 - 6 x + 9 - 4 x 2 + 4 x + 1 = 0
Giải phương trình
a
)
2
x
+
3
x
-
4
2
x
-
1
x
+
2
-
27
b
)
x
2
-
4
-
x
+
5...
Đọc tiếp
Giải phương trình
a ) 2 x + 3 x - 4 = 2 x - 1 x + 2 - 27
b ) x 2 - 4 - x + 5 2 - x = 0
c ) x + 2 x - 2 - x - 2 x + 2 = 4 x 2 - 4
d ) x + 1 x - 1 - x + 2 x + 3 + 4 x 2 + 2 x - 3 = 0
a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
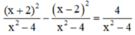
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
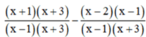
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
Đúng 0
Bình luận (0)
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)
\(x^2-4-\left(x+5\right)\left(2-x\right)=0\)
\(< =>\left(x-2\right)\left(x+2\right)+\left(x+5\right)\left(x-2\right)=0\)
\(< =>\left(x-2\right)\left(x+2+x+5\right)=0\)
\(< =>\left(x-2\right)\left(2x+7\right)=0\)
\(< =>\orbr{\begin{cases}x-2=0\\2x+7=0\end{cases}}< =>\orbr{\begin{cases}x=2\\x=-\frac{7}{2}\end{cases}}\)
Xem thêm câu trả lời
Xét dấu các biểu thức sau:
f(x)=x(16-4x2)
Giải các bất phương trình sau:
5-x/(x-3)(2x-1)<0
Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình sau:
a
)
4
x
2
+
2
x
−
5
0
b
)
9
x
2...
Đọc tiếp
Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình sau:
a ) 4 x 2 + 2 x − 5 = 0 b ) 9 x 2 − 12 x + 4 = 0 c ) 5 x 2 + x + 2 = 0 d ) 159 x 2 − 2 x − 1 = 0
a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: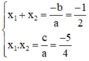 
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: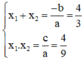 
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: 
Đúng 0
Bình luận (0)