Môđun của tổng hai số phức z 1 = 1 + 6 i và z 2 = 2 - 5 i là:
A. 32
B. 4
C. 10
D. 2 2
Môđun của hiệu hai số phức z 1 = 3 + 5 i và z 2 = - 1 + 2 i là:
A. 3
B. 5
C. 7
D. 7
Phần thực và phần ảo của số phức z thỏa mãn (1 - i)z - 1 + 5i = 0 là
A. 3 và –2
B. 3 và 2
C. 3 và – 2i
D. 3 và 2i
Ta có: (1 - i)z - 1 + 5i = 0 ⇔ (1 - i)z = 1 - 5i
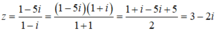
Vậy phần thực và phần ảo của z là 3 và -2
Chọn A
Đúng 0
Bình luận (0)
Giải các phương trình sau :
a) \(\left(3-2i\right)z+\left(4+5i\right)=7+3i\)
b) \(\left(1+3i\right)z-\left(2+5i\right)=\left(2+i\right)z\)
c) \(\dfrac{z}{4-3i}+\left(2-3i\right)=5-2i\)
a) Ta có (3 - 2i)z + (4 + 5i) = 7 + 3i <=> (3 - 2i)z = 7 + 3i - 4 - 5i
<=> z = <=> z = 1. Vậy z = 1.
b) Ta có (1 + 3i)z - (2 + 5i) = (2 + i)z <=> (1 + 3i)z -(2 + i)z = (2 + 5i)
<=> (1 + 3i - 2 - i)z = 2 + 5i <=> (-1 + 2i)z = 2 + 5i
z =
Vậy z =
c) Ta có + (2 - 3i) = 5 - 2i <=>
= 5 - 2i - 2 + 3i
<=> z = (3 + i)(4 - 3i) <=> z = 12 + 3 + (-9 + 4)i <=> z = 15 -5i
Đúng 0
Bình luận (0)
Tổng của hai số phức z 1 = 1 - 2 i , z 2 = 2 - 3 i là
A. 2 + 5i
B. 2 – 5i
C. 1 + 5i
D. 1 – 5i
Giải các phương trình sau: (1+3i)z-(2+5i)=(2+i)z
(1 + 3i)z - (2 + 5i) = (2 + i)z
⇔ (1 + 3i).z – (2 + i).z = 2 + 5i
⇔ [(1 + 3i) – (2 + i)].z = 2 + 5i
⇔ (-1 + 2i).z = 2 + 5i
Đúng 0
Bình luận (0)
Giải các phương trình sau trên tập số phức:
a) (1 + 2i)x – (4 – 5i) = –7 + 3i
b) (3 + 2i)x – 6ix = (1 – 2i)[x – (1 + 5i)]
a) (1 + 2i)x = − 3 −2i
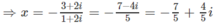
b) (2 − 2i)x = −(11 + 3i)
Đúng 0
Bình luận (0)
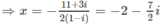
Thực hiện các phép tính:
a) (2 + 4i)(3 – 5i) + 7(4 – 3i);
b) (1 – 2i)2 – (2 – 3i)(3 + 2i).
Giải các phương trình sau: (3-2i)z+(4+5i)=7+3i
(3 - 2i)z + (4 + 5i) = 7 + 3i
⇔ (3 – 2i).z = (7 + 3i) – (4 + 5i)
⇔ (3 – 2i).z = 3 – 2i
⇔ z = 1.
Đúng 0
Bình luận (0)
Tìm phần ảo của số phức z thỏa mãn
(
1
-
3
i
)
z
¯
z
2
-
5
i
2
+
i
z
Đọc tiếp
Tìm phần ảo của số phức z thỏa mãn ( 1 - 3 i ) z ¯ z 2 - 5 i = 2 + i z
