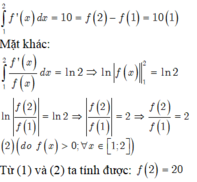Cho hàm số f(x) thỏa mãn f(f(x)) = x + 10. Biết f(2001) = 2011. Tính f(2011)

Những câu hỏi liên quan
cho hàm số f(x) thỏa mãn f(f(x)) = x + 10. Biết f(2001) = 2001. Tính f(2011)
Cho hàm số f(x) thỏa mãn f(f(x))=x+10. Biết f(2001)=2011. Tính f(2011)
có ai ko giúp mình với :))
hình như sai đề bài rồi bạn ơi
f(f(x)????
sửa lại đi mình làm cho
chúc bạn học tốt
>.<
Đúng 0
Bình luận (0)
a.Tìm các cặp số x,y thoả mãn\(|x^4-1|+|y^2-3|=0\)
b.Cho hàm số f(x) thoả mãn f(f(x))=x+10, biết f(2001)=2011
a, \(\left|x^4-1\right|\)\(+\left|y^2-3\right|=0\)
-Vì: $\left\{\begin{matrix}
|x^4-1|\geq 0 & \\
|y^2-3|\geq 0 &
\end{matrix}\right.$
-Để: $|x^4-1|+|y^2-3|=0$
-Thì:
$\Rightarrow \left\{\begin{matrix}
|x^4-1|=0 & \\
|y^2-3|=0 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x^4-1=0 & \\
y^2-3=0 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x^4=1 & \\
y^2=3 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x=\pm 1 & \\
y=\pm \sqrt{3} &
\end{matrix}\right.$
b, Đề thiếu kìa bạn!!
Đúng 0
Bình luận (0)
Bài 1 : Cho hàm số: y f(x) a.x2+b.x+c cho biết f(0)2010, f(1)2011, f(-1)2012, Tính f(-2).Bài 2 : Cho hàm số: y f(x) a.x2+b.x+c cho biết f(0)2010, f(1)2011, f(-1)2012, Tính f(-2).Bài 3 : Cho hàm số: y f(x) a.x2+b.x+c cho biết f(0)2010, f(1)2011, f(-1)2012, Tính f(-2).Bài 4 : Cho đa thức: f(x) x2-a.x-3 và g(x) (x3-x2-x-a-1)2015a, Tìm a biết -1 là 1 nghiệm của f(x)b, Với a tìm được ở câu a, Tìm nghiệm còn lại của f(x) và tính g(2).Bài 5: Cho hàm số y f(x) a.x2+b.x+c và biết f(0)2014, f(1)2015,...
Đọc tiếp
Bài 1 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 2 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 3 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 4 : Cho đa thức: f(x)= x2-a.x-3 và g(x)= (x3-x2-x-a-1)2015
a, Tìm a biết -1 là 1 nghiệm của f(x)
b, Với a tìm được ở câu a, Tìm nghiệm còn lại của f(x) và tính g(2).
Bài 5: Cho hàm số y= f(x)= a.x2+b.x+c và biết f(0)=2014, f(1)=2015, f(-1)=2017 ,
Tính f(-2).
Mọi người giúp mình với ạ mình đang cần gấp. Mình cảm ơn mọi người nhiều.
Bài 1 : làm tương tự với bài 2;3 nhé
Ta có : \(f\left(0\right)=c=2010;f\left(1\right)=a+b+c=2011\)
\(\Rightarrow f\left(1\right)=a+b=1\)
\(f\left(-1\right)=a-b+c=2012\Rightarrow f\left(-1\right)=a-b=2\)
\(\Rightarrow a+b=1;a-b=2\Rightarrow2a=3\Leftrightarrow a=\dfrac{3}{2};b=\dfrac{3}{2}-2=-\dfrac{1}{2}\)
Vậy \(f\left(-2\right)=4a-2b+c=\dfrac{4.3}{2}-2\left(-\dfrac{1}{2}\right)+2010=6+1+2010=2017\)
Đúng 4
Bình luận (0)
Cho hàm số y f(x) có đạo hàm liên tục trên [1;2] thỏa mãn
∫
1
2
f
(
x
)
d
x
10
và
∫
1
2
f
(
x
)
f
(
x
)...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên [1;2] thỏa mãn ∫ 1 2 f ' ( x ) d x = 10 và ∫ 1 2 f ' ( x ) f ( x ) d x = ln 2 . Biết rằng f(x)>0. Tính f(2)
A. f(2) = 10
B. f(2) = -20
C. f(2) = -10
D. f(2) = 20
cho hàm số y=f(x) thỏa mãn: f(x) + 3.f(2x)= x+1. Tính f(10)
Cho hàm số f(x)=ax^2+bx+c
biết f(0)=2010, f(1)=2011, f(-1)=2012. Tính f(-2)
\(f\left(0\right)=c=2010\)
\(f\left(1\right)=a+b+2010=2011\Rightarrow a+b=1\)(1)
\(f\left(-1\right)=a-b+2010=2012\Rightarrow a-b=2\)(2)
Từ (1) và (2) => a = 3/2; b = -1/2.
Vậy \(f\left(-2\right)=\frac{3}{2}\left(-2\right)^2-\frac{1}{2}\left(-2\right)+2010=6+1+2010=2017\)
Đúng 0
Bình luận (0)
cho f(x) thỏa mãn x.f(x-2011) = (x-2012).f(x)
CMR f(x) có 2 nghiệm khác nhau
cho hàm số y=f(x)=/x^2-2010x-2011/
Tính f(1),f(-2010)
Bài làm
Hàm số: y=f(x)=| x2 - 2010x - 2011 |
* Với f(1) = | 12 - 2010 x 1 - 2011 |
= | 1 - 2010 - 2011 |
= | -4020 |
= 4020
Vậy với f(1) thì = 420
* Với f(-2010) = | ( -2010 )2 - 2010 x ( -2010 ) - 2011 |
= | -4040100 - ( -4040100 ) - 2011 |
= | 0 - 2011 |
= - 2011
Vậy với f(-2010) thì bằng -2011
# Chúc bạn học tốt #.
Đúng 0
Bình luận (0)
\(y=f\left(x\right)=\left|x^2-2011x+x-2011\right|\)
\(y=f\left(x\right)=\left|x\left(x-2011\right)+\left(x-2011\right)\right|\)
\(y=f\left(x\right)=\left|\left(x+1\right)\left(x-2011\right)\right|\)
Thay vào mà tính thôi bạn
Đúng 0
Bình luận (0)