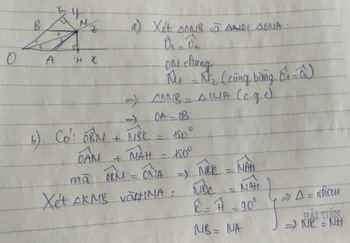Cho góc nhọn xOy = a. Từ 1 điểm M ở trog góc ta vẽ đc đg thẳng a song2 Oy, cắt Ox tại C. Từ M vẽ MH ⊥ Ox (H ∈ Ox). Tính số đó của góc tù tạo bởi đg thẳng a vs tia MH.

Những câu hỏi liên quan
Cho góc nhọn xoy và oz là tia phân giác của xoy.Qua điểm A thuộc tia õ, vẽ đường thẳng song song với oy cắt oz tại M.Qua M kẻ đường thẳng song song với ox cắt tại oy tại B.
A)Từ M vẽ MH vuông góc Ox(H thuộcOx),Mk vuông góc Oy(K thuộc Oy).Chứng minh MH=Mk.
B)Chứng minh Om vuông góc HK
Cho xOy < 90o có Oz là tia phân giác. Từ điểm M trên tia Oz, vẽ một đường thẳng song song với Oy cắt Ox tại A. Từ M vẽ đường thẳng song song Ox, cắt Oy tại B.
a) Chứng minh: OA = OB
b) Vẽ MH vuông góc Ox tại H , MK vuông góc Oy tại K. Chứng minh : MH = MK
c) Chứng minh OM là trung trực của AB
Cho góc nhọn xOy, Oz là tia phân giác của xOy. qua điểm A thuộc tia Ox vẽ đường thẳng song song với Oy cắt Oz tại M. Qua M kẻ đường thẳng song song với Ox cắt Oy tại B.Chứng minh:
a/OA=MB ; MA=OB.
b/ Từ M kẻ MH vuông góc với Ox ; MK vuông góc với Oy. Chứng minh MH=MK
Cho góc nhọn xOy có OZ là tia p/g của nó. Từ một điểm M trên tia OZ vẽ một đường thẳng song song với Oy. Từ M Vẽ một đường thẳng song song Ox, cắt oy tại b
a) CM: OA=OB
b) Vẽ MH vuông góc Ox tại H. MK vuông góc Oy tại K. CM MH=MK
c) CM OM là đường trung trực của AB
cho góc xOy nhọn, Oz là tpg, từ M trên Oz vẽ 1 đường thẳng song song với Oy cắt Ox tại A,từ M trên vẽ 1 đường thẳng song song với Ox cắt Oy tại B
a, Chứng minh OA= OB
b, Vẽ MH vuông góc với Ox tại H, MK vuông góc với Oy tại K. chứng minh MH= MK
c, Chứng minh OM là trung trực của AB
Bạn tự vẽ hình nhé .
a) Oz là phân giác góc xOy nên góc xOz = góc yOz
mà góc xOz = góc BMO(2 góc so le trong của Ox // MB) ; góc yOz = góc AMO (2 góc so le trong của Oy // MA)
=> góc AMO = góc BMO . \(\Delta OAM;\Delta OBM\)có góc AOM = góc BOM (cmt) ; chung cạnh OM ; góc AMO = góc BMO
=> \(\Delta OAM=\Delta OBM\left(g.c.g\right)\)=> OA = OB (2 cạnh tương ứng)
b) Từ gt ta có : \(\Delta OHM,\Delta OKM\)vuông tại H,K có góc HOM = góc KOM (cmt) ; chung cạnh OM
=> \(\Delta OHM=\Delta OKM\)(cạnh huyền - góc nhọn) => MH = MK (2 cạnh tương ứng)
c) OA = OB ( cmt) ; MA = MB (2 cạnh tương ứng của \(\Delta OAM=\Delta OBM\)) nên O,M thuộc trung trực của AB
=> OM là trung trực của AB
Đúng 0
Bình luận (0)
Cho góc nhọn xOy có Oz là phân giác của nó. Từ 1 điểm M, vẽ 1 đường thẳng song song với Oy. Từ M vẽ 1 đường thẳng song song Ox, cắt Oy tại B. Từ M vẽ 1 đường thẳng song song Oy, cắt Õ tại A
a) Chứng minh OA = OB
b) Vẽ MH vương góc Ox tại H, MK vuông góc Oy tại K. Chứng minh MH = MK
c) Chứng minh OM là trung trực của AB
Ai giải dc mk tick
Bài 1:
Cho góc xoy <90 độ có Oz là tia phân giác. Từ điểm M trên tia Oz, vẽ một đường thẳng song song với Oy cắt Ox tại A. Từ M vẽ đường thẳng song song Ox, cắt Oy tại B
a) Chứng minh OA = OB
b) Vẽ MH vuông góc với Ox tại H, MK vuông góc với Oy tại K. Chứng minh MH = MK
c) Chứng minh OM là trung trực của AB
cho góc nhọn xOy Oz là pg của góc xOy, M là 1 điểm bất kì thuộc Oz ( M k trùng vs C Qua M vẽ đg thẳng A vuông góc vs Ox tại A cắt oy tại C và vẽ đg thẳng B vuông góc Oy tại B cắt Ox tại D
a) AM = BM ( cm đc r )
b) tam giác BMC = tam giác AMD và tam giác DMC là tam giác cân ( cm đc r )
c) DM+AM<DC ( giúp câu này vs )
d) OM vuông góc vs CD ( cả câu này nữa )
cho góc nhọn xoy,tia oz là phân giác của góc đó.qua a thuộc ox vẽ đường thẳng song song oy cắt z tại m.qua m vẽ đường thẳng song song ox cắt oy tại m.a)chứng minh oa=ob,ma=mb b)từ m kẻ mh vuồng góc ox ,mk vuông góc oy.cm mk=mh
ai làm mình tick cho,cần gấp dã man quản lí ơi
Vì OA // MB (gt)
=> \(\widehat{AOM}\) = \(\widehat{OMB}\) (2 góc so le trong bằng nhau)
Vì AM // OB (gt)
=> \(\widehat{AMO}\)= \(\widehat{MOB}\) (2 góc so le trong bằng nhau)
Xét t/giác OAM và t/giác OMB , có:
OM : cạnh chung
\(\widehat{AOM}\)= \(\widehat{OMB}\)(cmt)
\(\widehat{AMO}\)= \(\widehat{MOB}\)(cmt)
Vậy t/giác OAM = t/giác OMB (c.g.c)
=> OA = OB (2 cạnh tương ứng bằng nhau)
=> MA = MB (2 cạnh tương ứng bằng nhau)
Vậy OA = OB
MA = MB
b) Vì Oz là tia phân giác của \(\widehat{xOy}\)
=> \(\widehat{HOM}\)= \(\widehat{MOK}\)= \(\frac{\widehat{xOy}}{2}\)(t/c)
Vậy \(\widehat{HOM}\)= \(\widehat{MOK}\)
Từ gt , ta có :
t/giác OHM và tam giác OKM vuông góc tại H;K
=> \(\widehat{MHO}\)= 90 độ; \(\widehat{MKO}\)= 90 độ
=> \(\widehat{MHO}\)= \(\widehat{MKO}\)
Xét t/giác OHM và t/giác OKM , có:
OM : cạnh chung (gt)
\(\widehat{HOM}\)= \(\widehat{MOK}\)(cmt)
\(\widehat{MHO}\)= \(\widehat{MKO}\)(cmt)
Vậy t/giác OHM = t/giác OKM (g.c.g)
=> MH = MK (2 cạnh tương ứng bằng nhau) (=> đpcm)
Vậy MH = MK
Đúng 0
Bình luận (0)