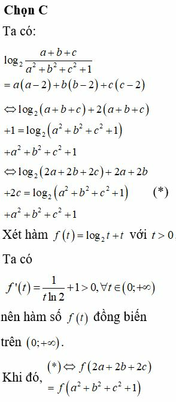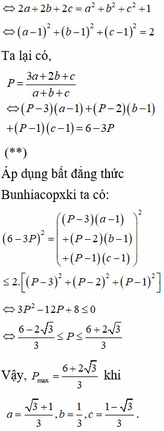tìm giá trị thích hợp của a,b : aa,bxa,b =aa,bb

Những câu hỏi liên quan
Tìm giá trị của a và b sao cho a,b x 9,9 = aa,bb
abx99=aabb=11xa0b =>abx9=a0b =>90a+9b=100a+b =>10a=8b =>5a=4b => a=4 va b=5.
Đúng 0
Bình luận (0)
Tìm giá trị của a và b sao cho a,b x 9,9 = aa,bb
abx99=aabb=11xa0b
=>abx9=a0b
=>90a+9b=100a+b
=>10a=8b
=>5a=4b
=> a=4 va b=5.
Đúng 0
Bình luận (0)
Chọn phát biểu sai.A. Tập hợp các ước của aa là Ư(a)Ư(a), tập hợp các bội của aa là B(a)B(a).B. Nếu số tự nhiên aa chia hết cho số tự nhiên bb thì ta nói aa là ước của bb, còn bb là bội của aa.C. Ta có thể tìm các bội của một số khác 00 bằng cách nhân số đó lần lượt với 0;1;2;3;...0;1;2;3;....D. Ta có thể tìm các ước của a (a1)a (a1) bằng cách lần lượt chia aa cho các số tự nhiên từ 11 đến aa để xem aa chia hết cho những số nào, khi đó các số ấy chính là ước của aa.
Đọc tiếp
Chọn phát biểu sai.
A. Tập hợp các ước của aa là Ư(a)Ư(a), tập hợp các bội của aa là B(a)B(a).
B. Nếu số tự nhiên aa chia hết cho số tự nhiên bb thì ta nói aa là ước của bb, còn bb là bội của aa.
C. Ta có thể tìm các bội của một số khác 00 bằng cách nhân số đó lần lượt với 0;1;2;3;...0;1;2;3;....
D. Ta có thể tìm các ước của a (a>1)a (a>1) bằng cách lần lượt chia aa cho các số tự nhiên từ 11 đến aa để xem aa chia hết cho những số nào, khi đó các số ấy chính là ước của aa.
cho a>b>1, tìm chữ số thích hợp thay vào a và b trong biểu thức sau:
aa nhân bb = 3267
aa x bb = 3267
(10a+a) x (10b+b) = 3267
11a x 11b = 3267
a x b = 3267 : 11 : 11 = 27
Có : 27 = 1 x 27 = 3 x 9
=> a=9;b=3 ( vì a,b là các chữ số và a > b > 1 )
Tk mk nha
Đúng 0
Bình luận (0)
\(\overline{aa}\times\overline{bb}=11a\times11b=121ab=3267\)
\(\Rightarrow ab=27=3.9=9.3\)
Vậy a=3,b=9 hoặc a=9,b=3
Đúng 1
Bình luận (0)
Ta có : aa x bb = 3267
10a + a x 10b + b = 3267
11a x 11b = 3267
112 x a x b = 3267
a x b = 27
\(\Rightarrow\)a = 9 ; b = 3 ( vì a > b > 1 )
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho a,b,c là các số thực dương thỏa mãn:ab+bc+ac=3abc
Tìm giá trị nhỏ nhất của biểu thức K=\(\frac{a^2}{c\left(cc+aa\right)}\)+\(\frac{a^2}{a\left(aa+bb\right)}\)+\(\frac{c^2}{b\left(bb+cc\right)}\)
Cho a > b > 1. Tìm chữ số thích hợp thay vào a và b trong biểu thức sau:
aa*bb=3267
Cho a,b,c là các số thực thỏa mãn
log
2
a
+
b
+
c
a
2
+
b
2
+
c
2
+...
Đọc tiếp
Cho a,b,c là các số thực thỏa mãn log 2 a + b + c a 2 + b 2 + c 2 + 1 = a a - 2 + b b - 2 + c c - 2 Tìm giá trị lớn nhất của biểu thức P = 3 a + 2 b + c a + b + c
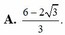
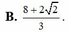
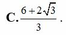
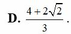
tìm a,b,c và giải thích
\(\overline{aa}\)+\(\overline{bb}\)+\(\overline{cc}\)=\(\overline{bac}\)
Lời giải:
\(\overline{aa}+\overline{bb}+\overline{cc}=\overline{bac}\)
\(11.a+11.b+11c=100b+10a+c\)
\(89b=a+10c=\overline{ca}\)
Vì $\overline{ca}$ là số có 2 chữ số nên $89b$ cũng chỉ có 2 chữ số. Nếu $b\geq 2$ thì $89b>100$ (vô lý) nên $b< 2$
Nếu $b=1$ thì $\overline{ca}=89\Rightarrow c=8; a=9$
Nếu $b=0$ thì $\overline{ca}=0\Rightarrow c=a=0$ (loại)
Vậy $a=9; b=1; c=8$
Đúng 0
Bình luận (1)
Dựa vào minh họa hình học (xét vị trí tương đương đối của hai đường thẳng xác định bởi hai phương trình trong hệ) , em hãy giải thích các kết luận sau:Hệ phương trình
a
x
+
b
y
c
a
x
+...
Đọc tiếp
Dựa vào minh họa hình học (xét vị trí tương đương đối của hai đường thẳng xác định bởi hai phương trình trong hệ) , em hãy giải thích các kết luận sau:
Hệ phương trình a x + b y = c a ' x + b ' y = c ' (a,b,c,a',b',c' khác 0)
- Có vô số nghiệm nếu a a ' = b b ' = c c ' ;
- Vô nghiệm nếu a a ' = b b ' ≠ c c ' ;
- Có một nghiệm duy nhất nếu a a ' ≠ b b '
Ta biết tập nghiệm của phương trình ax + by = c được biểu diễn bằng đường thẳng ax + by = c và tập nghiệm của phương trình a'x + b'y = c' được biểu diễn bằng đường thẳng a'x + b'y = c'.

Đúng 0
Bình luận (0)