Bài 1: Qui đồng mẫu các phân thức sau:
a) \(\frac{3}{2x-6};\frac{1}{3x-6}\)
b) \(\frac{1}{2x^2-8x+8};\frac{1}{3\left(x-2\right)};\frac{1}{x^2-x-2}\)
Giúp đỡ e vs mn :((
Những câu hỏi liên quan
Đề bài: Quy đồng mẫu thức các phân thức sau (có thể áp dụng quy tắc đổi dấu đối với một phân thức để tìm mẫu thức chung thuận tiện hơn):
a) \(\frac{4x^2-3x+5}{x^3-1};\frac{1-2x}{x^2+x+1};-2\)
b) \(\frac{10}{x+2};\frac{5}{2x-4};\frac{1}{6-3x}\)
Làm ơn giải chi tiết nha, mình cảm ơn nhìu~~~
Qui đồng mẫu thức các phân thức sau (có thể áp dụng qui tắc đổi dấu với các phân thức để tìm mẫu thức chung thuận tiện hơn):
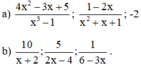
a) + Phân tích mẫu thức thành nhân tử để tìm nhân tử chung:
x3 – 1 = (x – 1)(x2 + x + 1)
x2 + x + 1 = x2 + x + 1
⇒ MTC = (x – 1)(x2 + x + 1) = x3 – 1
+ Nhân tử phụ : (Có thể bỏ qua bước này nếu đã quen)
(x3 – 1) : (x3 – 1) = 1
(x3 – 1) :( x2 + x + 1) = x - 1
(x3 – 1) : 1 = x3 – 1
+ Quy đồng :
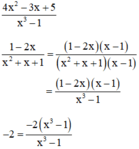
b) Ta có:
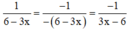
+ Phân tích mẫu thức thành nhân tử để tìm MTC
x + 2 = x + 2
2x – 4 = 2.(x – 2)
3x – 6 = 3.(x – 2)
⇒ MTC = 6.(x + 2)(x – 2)
+ Nhân tử phụ: (Có thể bỏ qua bước này nếu đã quen)
6(x + 2)(x – 2) : (x + 2) = 6(x – 2)
6(x + 2)(x – 2) : 2(x – 2) = 3(x + 2)
6(x + 2)(x – 2) : 3(x – 2) = 2(x + 2)
+ Quy đồng:
Đúng 0
Bình luận (0)
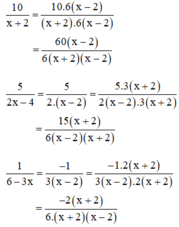
Qui đồng mẫu thức các phân thức:
\(\dfrac{x}{x^2+2x-15};\dfrac{1}{x^2+5x-6}\) và \(\dfrac{1}{-x^2+4x-3}\)
quy đồng mẫu các phân thức sau
a,3x/x^3-1, 1-2x/4x^2+x+1 b, x/3x+6, 2/x^2+2x
Qui đồng mẫu số các phân số sau:
a,3/5 và 5/6; b, 6/13 và 9/26; c,1/2;2/5 và 5/6
Quy đồng mẫu thức các phân thức sau
\(\frac{x}{x^6-27};\frac{2x}{x^2-6x+9};\frac{1}{x^2+3x+9}\)
Giúp mình với ạ
Qui đồng mẫu thức các phân thức:
\(\dfrac{2}{x^3-y^3}\) và \(\dfrac{2x+1}{x^2-y^2}\)
Qui đồng mẫu thức các phân thức:
\(\dfrac{2}{x^3-y^3};\dfrac{1}{x+y}\) và \(\dfrac{2x+1}{x^2-y^2}\)
Ta có \(\frac{2}{x^3-y^3}=\frac{2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{2x-1}{x^2-y^2}=\frac{2x+1}{\left(x+y\right)\left(x-y\right)}\)
\(\frac{1}{x+y}\) giữ nguyên
MTC: \(\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)\)
Các nhân tử phụ tương ứng là : \(\left(x+y\right);\left(x-y\right)\left(x^2+xy+y^2\right);\left(x^2+xy+y^2\right)\)
Ta có:
\(\frac{2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\frac{2.\left(x+y\right)}{\left(x-y\right)\left(x+y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{1}{x+y}=\frac{1.\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{2x+1}{\left(x+y\right)\left(x-y\right)}=\frac{\left(2x+1\right)\left(x^2+xy+y^2\right)}{\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)}\)
Đúng 0
Bình luận (0)
Qui đồng mẫu thức các phân thức:
\(\dfrac{1}{2x^2+3x-5}\) và \(\dfrac{x+2}{4x-x^2-3}\)
\(\frac{x+2}{4x-x^2-3}=\frac{-\left(x+2\right)}{x^2-4x+3}=\frac{\left(-x-2\right)\left(2x+5\right)}{\left(x-1\right)\left(x-3\right)\left(2x+5\right)}=\frac{-2x^2-9x-10}{\left(x-1\right)\left(x-3\right)\left(2x+5\right)}\)
\(\frac{1}{2x^2+3x-5}=\frac{1}{\left(x-1\right)\left(2x+5\right)}=\frac{x-3}{\left(x-1\right)\left(x-3\right)\left(2x+5\right)}\)
Đúng 0
Bình luận (0)