Hỏi cái gì ???

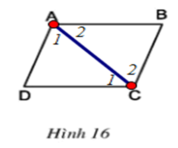
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)

Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)

Xét ΔABC và ΔCDA có:

∠A2 = ∠C1 (cmt)

AC chung

∠A1 = ∠C2 (cmt)

⇒ ΔABC = ΔCDA (g.c.g)

⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)

b)

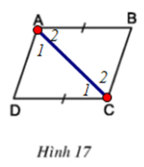
Xét ΔABC và ΔCDA có:

AC chung

∠A2 = ∠C1 (cmt)

AB = CD

⇒ ΔABC = ΔCDA (c.g.c)

⇒ AD = BC (hai cạnh tương ứng)

∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)

tự vẽ hình

a)  Xét tam giác DAC và tam giác BCA có:

    góc DAC = góc BCA  (slt do AD // BC)

    AC:  chung

    góc DCA = góc BAC (slt do AB // DC)

suy ra: tam giác DAC = tam giác BCA  (g.c.g)

=>  AD = BC; DC = AB

b)  Xét tam giác DAC và tam giác BCA có:

   AD = AB

  góc DCA = góc BAC (slt do AB // CD)

  AC: chung

suy ra: tam giác DAC = tam giác BCA   (c.g.c)

=>  AD = BC

      góc DAC = góc BCA

mà 2 góc này slt

=>  AD // BC

tks bạn nha

a) Ta có : AB // CD ( do ABCD là hình thang )

           AD // BC ( gt )

=> ABCD là hình bình hành 

=>  AD = BC ; AB = CD

b) Ta có : AB = CD ( gt )

              AB // CD ( gt )

=> ABCD là hình bình hành 

=> AD // BC ; AD = BC