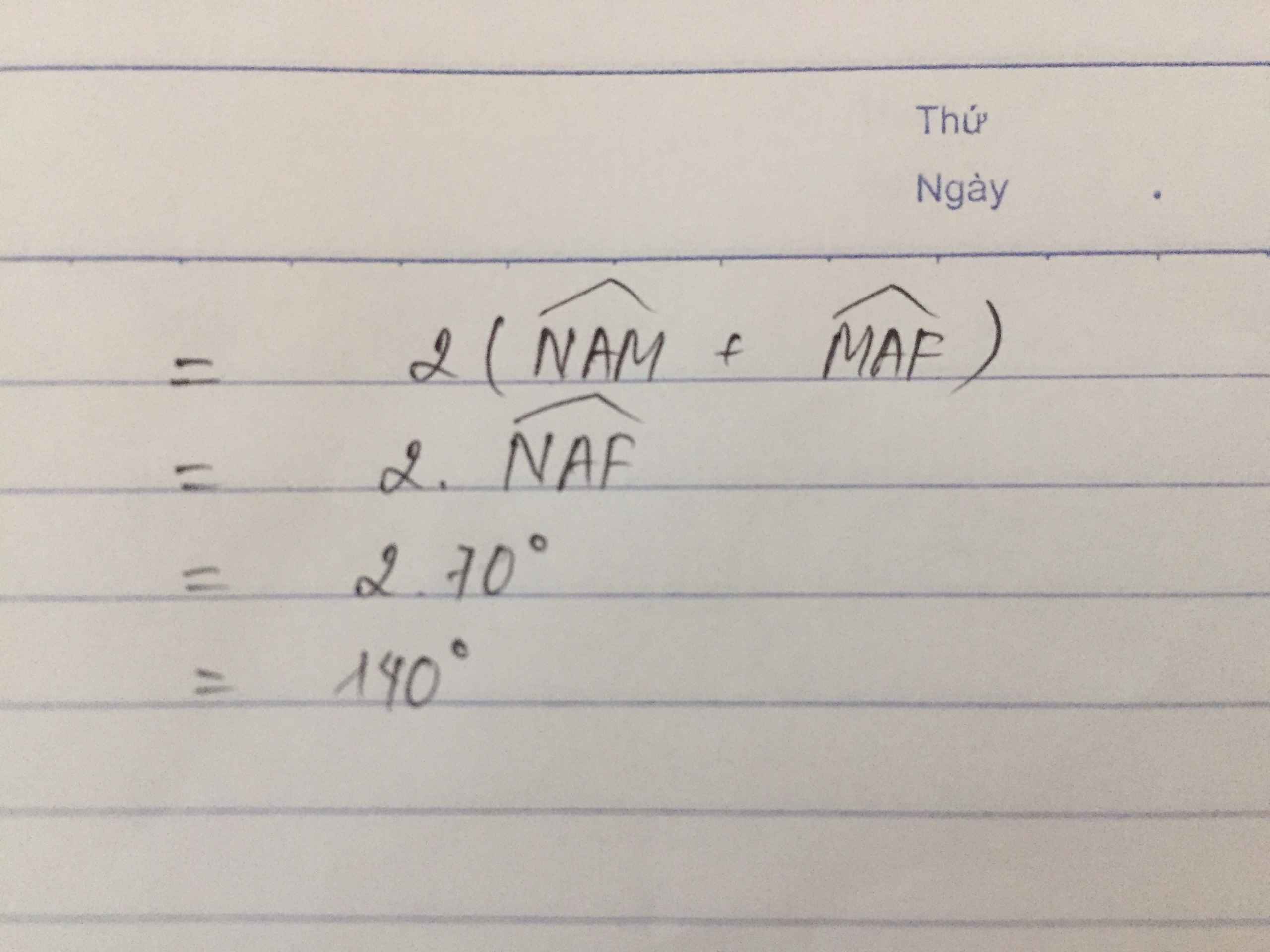Bài 1. Cho △ABC: góc A=70 độ. M thuộc BC, D đối xứng M qua AB, E đối xứng với M qua AC"
a)CMR: AD=AE.
b)Tính góc DAE?
Bài 2. Cho △ABC nhọn: góc A=60 độ, trực tâm H. Gọi M là điểm đối xứng với H qua BC
a)CMR: △BHC=△BMC
b)Tính góc BMC?
P/s: Mong các bạn giải giúp mk với !!!!!!