hình thang ABCD 

=> AD=BC = 3cm ( định lí 1 )

AB//CD ( ABCD là hình thang cân )

=> góc B1 = góc D2 ( SLT )

     góc D1 = góc D2 ( gt )

=> góc B1 = góc D1 

=> tg ABD cân tại A

=> AD=AB= 3cm

tg DBC vuông ở B

hình thang cân ABCD 

=> góc D = góc C

   2 lần góc D1  = góc C

=> góc DBC = góc D1 + 2 lần góc D1 = 90 độ

                                       3 lần góc D1 = 90 độ

=>                                            góc D1 = 900 : 3 

                                                             = 300

=> góc C = 900 - góc D1 = 900 - 300 = 600

Gọi DA giao CB tại O

tg ODC có DB là pgiác 

BD vuông góc với Oc

=> tg ODC cân ở D

lại có góc C = 60 độ

=> tg OCD đều

=> CD = CO

mà tg ODC đều nên DB là đường phân giác đồng thời là đường trung tuyến

=> OB= BC

     CD= CO = OB+BC

mà OB = BC ( cmt )

=> CĐ= CƠ = 2CB = 2.3 = 6 ( cm )

Chu vi của hình thang cân ABCD là

AB+BC+AD+CD = 3+3+3+6= 15 (cm )

Bạn ơi vẽ hình hộ mk đc ko ạ ?

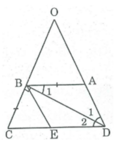
Ta có: AD = BC = 3 (cm) (tính chất hình thang cân)

∠ (ABD) =  ∠ (BDC) (so le trong)

∠ (ADB) =  ∠ (BDC) ( do DB là tia phân giác của góc D )

⇒ ∠ (ABD) =  ∠ (ADB)

⇒ ∆ ABD cân tại A

⇒ AB = AD = 3 (cm)

∆ BDC vuông tại B

∠ (BDC) +  ∠ C = 90 0

∠ (ADC) =  ∠ C (gt)

Mà  ∠ (BDC) = 1/2  ∠ (ADC) nên  ∠ (BDC) = 1/2  ∠ C

∠ C + 1/2  ∠ C =  90 0  ⇒  ∠ C =  60 0

Từ B kẻ đường thẳng song song AD cắt CD tại E.

Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE

⇒ DE = 3 (cm), BE = 3 (cm)

∠ (BEC) =  ∠ (ADC) (đồng vị)

Suy ra: ∠ (BEC) =  ∠ C

⇒ ∆ BEC cân tại B có  ∠ C =  60 0

⇒ ∆ BEC đều

⇒ EC = BC = 3 (cm)

CD = CE + ED = 3 + 3 = 6(cm)

Chu vi hình thang ABCD bằng:

AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)

ABCD là hình thang cân (gt) nên AB song song với CD,AD=BC=6cm và góc C=góc ADC

DB la tia p/g của góc ADC(gt) nên góc ADB=góc BDC= 1/2 góc ADC =1/2 góc C

AB song song với CD (cmt) suy ra: góc ABD=góc BDC

Tam giác ABD có: góc ABD=góc ADB(=góc BDC)

Do đó tam giác ABD cân tại A (DHNB) suy ra: AB=AD=6cm

Tam giác DBC vuông tại B nên góc BDC+góc C=90 độ

Hay 1/2 góc C+ góc C=90 độ

3/2 góc C =90 độ

C=60 độ.Sau đó tính được góc BDC=30 độ

Tam giác BDC vuông tại B có góc BDC=30 độ vì thế BC=1/2 DC

Do đó:DC=2BC=2x6=12(cm)

Chu vi hình thang ABCD là:

                             AB+AD+BC+CD=6+6+6+12=30(cm)

Vậy chu vi hình thang ABCD là 30 cm

P/s chu vi hình thang 30 cm :)))))

Bài 2:

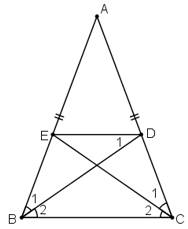
Ta có: ∆ABC là ∆ cân tại A(gt)

=>∠ABC=∠ACB

+Ta có BD là tia pgiac của ∠ABC

=>∠B₁=∠B₂=1/2∠ABC

+Ta có CE là tia pgiac ∠ACB

=>C₁=C₂=1/2∠ACB

Xét ∆

AEC và ΔADB có:

+∠A chung

+AB=AC

+C₁=B₁

=> ΔAEC = ΔADB

=> AE = AD

=>BCDE là hình thang cân

b) Ta có ∠ACB=∠ABC=50^o(do BCDE là hình thang cân)

Ta có: ED//BC

\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABC}=\widehat{AED}\\\widehat{ACB}=\widehat{ADE}\end{matrix}\right.=50^o}\) (SLT)

Mà ∠DEB=∠EDC

Ta có:

+∠DEB+∠AED=180^o (kề bù)

=>50^o+∠AED=180^o

=>∠AED=180^o-50^o=130^o

=>∠AED=∠ADE=130^o

Bài 1:

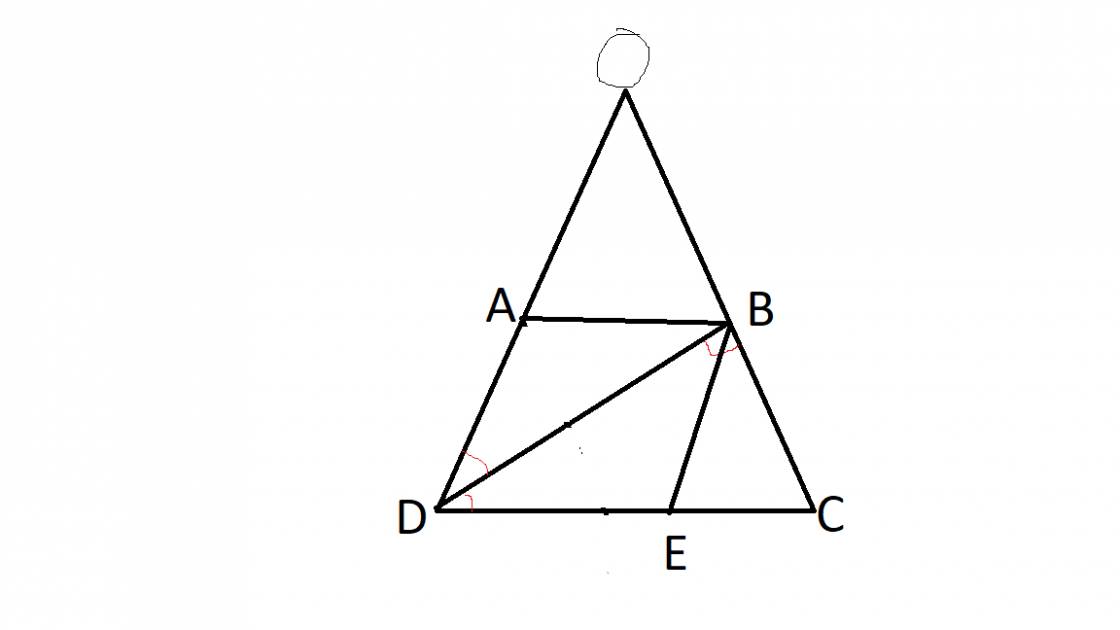
Ta có: AD=BC=3cm (t/c hthang)

Vì AB//CD(gt) nên \(\widehat{ABD}=\widehat{BDC}\left(SLT\right)\)

Mà \(\widehat{ADC}=\widehat{BDC}\) (do BD là tia pgiac góc D)

=>∠ABD=∠BDC 

=>∆ABD cân tại A

=>AD=BC=3cm

Vì ∆DBC vuông tại B

nên ∠BDC+∠C=90^o

Mà ∠ADC=∠C (do ABCD là hình thang cân)

và ∠BDC=1/2 ∠ADC

=> ∠BCD=1/2∠C

Khi đó: ∠C+1/2∠C=90^o=>∠C=60^o

- Kẻ từ B 1 đường thẳng // AD cắt CD tại E

Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE

⇒ DE = 3 (cm), BE = 3 (cm)

Mà ∠BEC=∠ADC(đồng vị)

=>∠BEC=∠C

=>∆BEC cân tại B có ∠C=60^o

=>∆BEC là ∆ cả cân cả đều

=> EC=BC=3cm

Ta có: CD = CE + ED = 3 + 3 = 6(cm)

Chu vi hình thang ABCD bằng:

AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)

Xét \(\Delta\)ABD có: \(\widehat{ABD}\) = \(\widehat{BDC}\) ( hai góc so le trong)

                         \(\widehat{ADB}\) = \(\widehat{BDC}\) (BD là phân giác của góc \(\widehat{ABD}\))

            ⇒          \(\widehat{ABD}\) =  \(\widehat{ADB}\) (vì cùng bằng góc BDC)

             ⇒          \(\Delta\) ABD cân tại A ⇒ AB = AD = 3 cm

Gọi E là trung điểm của DC ta có:\(\Delta\)BCD vuông tại B nên

BE = DE = EC (trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)

Mặt khác ta có: \(\widehat{ADC}\) = \(\widehat{DCB}\) ( vì ABCD là hình thang cân)

⇒\(\widehat{BDC}\) = \(\dfrac{1}{2}\) \(\widehat{DCB}\) ⇒ \(\widehat{DCB}\) + \(\dfrac{1}{2}\)\(\widehat{DCB}\) = 90⁰ 

⇒ \(\widehat{DCB}\) \(\times\) ( 1 + \(\dfrac{1}{2}\)) = 90⁰

⇒ \(\widehat{DCB}\) = 90⁰ : \(\dfrac{3}{2}\) = 60⁰ 

Xét \(\Delta\)BCE có BE = EC và  \(\widehat{BCE}\) = 60⁰ nên \(\Delta\)BCE là tam giác đều

⇒ BE = EC = BC = 3 cm 

⇒ DC = BE \(\times\) 2 = 3 \(\times\) 2 = 6 cm

Chu vi của hình thang ABCD là:

3 + 3 + 6 + 3 = 15 (cm)

Kết luận chu vi hình thang là: 15 cm