Một đội xe tải trong 3 ngày phải chuyển hết một số hàng hóa 2 ngày đầu độc chất thải đã chuyển được 13,14 số hàng hóa biết rằng ngày thứ hai đội chuyển được 3/7 số hàng hóa vận chuyển ít hơn ngày thứ nhất 30 tấn hỏi ngày thứ ba đôi chân bao nhiêu hàng hóa

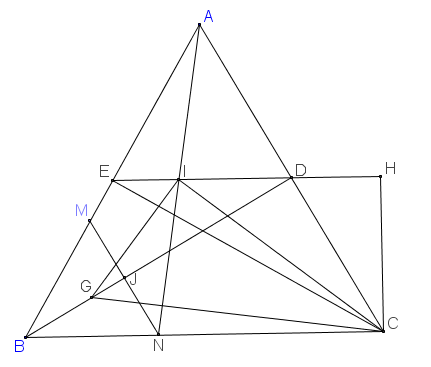
Gọi E, D lần lượt là trung điểm AB, AC, ta có I, E, D thẳng hàng
MN cắt BD tại J, hạ CH vuông góc ED tại H
Có DH=DC2=ED2DH=DC2=ED2
=>EDEH=23EDEH=23
Có BGBD=BGBJ.BJBDBGBD=BGBJ.BJBD
=23.BNBC=EDEH.EIED=23.BNBC=EDEH.EIED
=>BGBD=EIEHBGBD=EIEH
<=>BGEI=BDEHBGEI=BDEH (1)
Ta có △CBD∼△CEH△CBD∼△CEH (g, g)
=>CBCE=BDEH=BGEICBCE=BDEH=BGEI
=>△CBG∼△CEI△CBG∼△CEI (c, g, c) (2)
(2) =>ˆBCG=ˆECIBCG^=ECI^
<=>ˆBCG+ˆGCE=ˆGCE+ˆECIBCG^+GCE^=GCE^+ECI^
<=>ˆBCE=ˆGCIBCE^=GCI^ (3)
(2) =>BCEC=GCICBCEC=GCIC (4)
từ (3, 4) =>△BEC∼△GIC△BEC∼△GIC (c, g, c)
=>ˆI=90∘I^=90∘, ˆG=60∘G^=60∘ (đpcm)

Hình gửi kèm

youtube.com/c/AnimeVietsubchannel

pokemon pikachu tự nhiên ghi z dẹ

BG cắt MN,AC lần lượt tại K và E. 
MG cắt BC tại H. 
nếu vẽ hình chính xác thì sẽ nhận ra ngay là I = 90 và I,E,C,H,G nội tiếp trong một đường tròn. giờ ta khai thác cái này trước. 

BM=MN;B=60 =>BMN đều, có G là trọng tâm => MH_|_BC và BK_|_MN (hay BE_|_AC); K,H là trung điểm MN,BN 
E và H nhìn GC dưới góc 90 độ => nội tiếp đường tròn đường kính GC (*) 

I và K là trung điểm AN và MN=> IK//AB 
tương tự, KH//AB 
=> I,K,H thẳng hàng. => góc IKE= góc GKH(1) 

I,E là trung điểm AN,AC=> IE//BC => góc IEK= góc KBH (a) 
góc KBH =góc HMN (cùng phụ góc MNB) = góc HMB (MH là phân giác)= góc GHK (so le trong)(b) 
(a),(b) => góc IEK = góc GHK (2) 
(1),(2) => góc EGH= góc HIE 
I và G cùng nhìn HE dưới một góc bằng nhau => thuộc cùng một đường tròn(**) 
(*),(**) => góc GIC =90. 
hai góc còn lại sẽ hơi bị khủng. 
gọi F là trung điểm GC. lại có E là trung điểm AC => FE/AG= EC/AC =1/2(c) 
lấy A' đối xứng với A qua G; N' đối xứng với N qua G=>AN'A'N là hình bình hành 
gọi B' là giao điểm của NN' và AB 

ta có NG=2B'G=N'G vậy B' là trung điểm N'G mà AB' _|_ N'G vậy góc AN'G = góc AGN'= góc NGA' 
AN'A'N là hình bình hành => góc AN'N = góc N'NA' 
vậy tam giác A'GN cân tại A' => A'N=A'G=AG(e) 

G và I là trung điểm AA' và AN => GI/A'N=AG/AA' = 1/2(d) 
(c),(d)(e) => GI=EF=1/2 GC mà GIC là tam giác vuông tại I => G=60;C=30

Hoặc google thẳng tiến là ok

a) Xét tam giác NAB và tam giác NEM có                                                                                                                                     AN=EN; BN=MN; góc ENM =góc BNA =>2 tam giác bằng nhau                                                                                                      b)ta có BC=2Ab => Bc/2 = AB => BM=cm=ma                                                                                                                                        =>tam giác MAb cân tại b

để mk t.i.c.k cho nguyễn bảo ngọc nha

a) Ta có

+)AM=AB-BM=6-3,75=2,25

+)MN//BC => \(\frac{AN}{AC}=\frac{AM}{AB}\)=> \(\frac{AN}{8}=\frac{2,25}{6}=\frac{3}{8}\)

=> AN=3(cm)

CN=AC-AN=8-3=5(cm)

b) +)MK//BI => \(\frac{MK}{BI}=\frac{AK}{AI}\left(1\right)\)

+) NK//CI => \(\frac{NK}{CI}=\frac{AK}{AI}\left(2\right)\)

(1)(2) => \(\frac{MK}{BI}=\frac{NK}{CI}\)mà MK=NK (K là trung điểm MN)

=> BI=CI => I là trung điểm BC

c) \(\Delta\)ABC vuông tại A

=> BC²=AB²+AC²=6²+8²=10² (Định lý Pytago)

=> BC=10cm

Ta có: \(\hept{\begin{cases}\frac{AN}{CN}=\frac{3}{5}\\\frac{AB}{BC}=\frac{6}{10}=\frac{3}{5}\end{cases}\Rightarrow\frac{AN}{CN}=\frac{AB}{AC}=\frac{3}{5}}\)

=> BN là phân giác \(\widehat{ABC}\)