theo định lý pytaogo thì : tổng bình phương 2 cạnh góc vuông = bình phương cạnh huyền nên bình phương cạnh huyền lớn hơn bình phương 2 cạnh góc vuông (ko phải tổng nhé)=> cạnh huyền là cạnh lớn nhất trong tam giác vuông .

 Tk mình nha , chúc bạn học tốt

1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.

2. -Có 3 trường hợp bằng nhau của 2 tam giác:

+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).

+Trường hợp 2: cạnh-góc-cạnh(c.g.c).

+Trường hợp 3: góc-cạnh-góc(g.c.g)

3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông

4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau

-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau

+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân

- Cách chứng minh 1 tam giác là tam giác cân:

+ Chứng minh tam giác có 2 cạnh bằng nhau

+ Chứng minh tam giác có 2 góc bằng nhau

+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)

5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau

- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ

+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều

+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều

- Cách chứng minh 1 tam giác là tam giác đều:

+Chứng minh tam giác có 3 cạnh bằng nhau

+Chứng minh tam giác có 3 góc bằng nhau

+Chứng minh tam giác có 2 góc có 60 độ

+Chứng minh tam giác cân có 1 góc có 60 độ

6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông

- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông

1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.

2. -Có 3 trường hợp bằng nhau của 2 tam giác:

+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).

+Trường hợp 2: cạnh-góc-cạnh(c.g.c).

+Trường hợp 3: góc-cạnh-góc(g.c.g)

3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông

4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau

-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau

+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân

- Cách chứng minh 1 tam giác là tam giác cân:

+ Chứng minh tam giác có 2 cạnh bằng nhau

+ Chứng minh tam giác có 2 góc bằng nhau

+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)

5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau

- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ

+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều

+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều

- Cách chứng minh 1 tam giác là tam giác đều:

+Chứng minh tam giác có 3 cạnh bằng nhau

+Chứng minh tam giác có 3 góc bằng nhau

+Chứng minh tam giác có 2 góc có 60 độ

+Chứng minh tam giác cân có 1 góc có 60 độ

6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông

- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông

Xếp các tam giác vuông = nhau như hình vẽ:

Ta có: \(S_{BCDE}=S_{AMPN}+4.S_{ABC}\)

\(\Rightarrow a^2=\left(c-d\right)^2+4.\frac{bc}{2}\)

\(\Leftrightarrow a^2=c^2-2.bc+b^2+2.bc\)

\(\Leftrightarrow a^2=c^2+b^2\)

P/s: Còn nhiều cách.

Đây cũng là một cách chứng minh được giới thiệu trong cuốn sách của Elisha Scott Loomis. Ann Condit nghĩ ra cách chứng minh này vào năm 1938 khi cô mới 16 tuổi và là sinh viên của trường trung học ở miền nam Ấn Độ.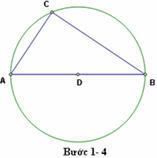

Dựng hình và kiểm tra

1. Dựng đoạn thẳng AB.

2. Vẽ trung điểm D của đoạn thẳng này

3. Vẽ đường tròn bán kính DA.

4. Vẽ đoạn BC và AC , với C là một điểm nằm trên đường tròn. Như vvậy ta đã dựng được tam giác vuông ABC vuông tại C.

5. Vẽ các hình vuông trên các cạnh của tam giác vuông ABC.

6. Vẽ các trung điểm L, M, N của các cạnh phía ngoài của các hình vuông.

7. Vẽ các đoạn DL, DM, DL.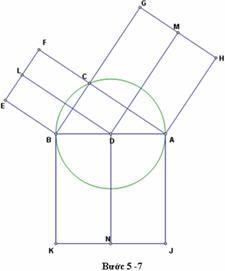

8. Vẽ đoạn FG, Vẽ tia DC, và điểm P là giao điểm cuat tia DC và đoạn FG, sau đó làm ẩn đi tia DC và hiện đoạn DP.

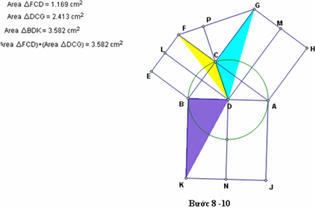
9. Tô màu khác nhau cho diện tích các tam giác DCF, DCG, và DBK.

Cách chứng minh này đưa ra mối liên quan giữa diện tích của các hình tam giác được tô màu với diện tích của các hình vuông trên các cạnh tam giác vuông.

Chọn menu Measure --> calculate để tính được tỉ lệ diện tích của các tam giác với các hình vuông tương ứng.

10. Đo diện tích các tam giác, và di chuyển điểm C quanh một nửa đường tròn trên đường kính AB.

Ta nhận thấy: tổng diện tích của 2 tam giác nhỏ luôn bằng diện tích của tam giác lớn hơn. Và tổng diện tích này không đổi khi điểm C chuyển động trên đường tròn. (xem hình bên dưới).
 

♥Trên mạng nha..Bn tham khảo nhé♥

cảm ơn bạn nha

\(a^2=b^2+c^2-2bc.\cos A\)

=> cosA =0 => A =90

Sách giáo khoa có viết bạn ak,nếu ko hiểu mình làm lại cho

Một số cách chứng minh định lí Pitago Cách 1: Chứng minh của E. A. CoolidgeCách chứng minh này xuất hiện trong cuốn sách về các vấn đề kinh điển thuộc học thuyết Pitago của tác giả Elisha Scott Loomis, được xuất bản lần đầu tiên bởi Hội đồng giáo viên quốc gia của môn toán học, vào năm 1927. Thật đáng tiếc, quyển sách này hiện nay không được xuất bản nữa, trong cuốn sách này có tới trên 300 cách chứng minh định lý Pitago, trong đó, có nhiều cách chứng minh tương tự nhau, và tất cả các cách chứng minh nổi tiếng đều có trong cuốn sách của Loomis.Cách chứng minh dưới đây thì tương tự như cách chứng minh của Bhaskara trong phần “Behold!” đã giới thiệu ở bài trước. Cách chứng minh này được đăng trên tạp trí giáo dục, xuất bản hàng ngày, và tác giả của nó là cô E. A. Coolidge - là một người mù.Dựng hình và kiểm tra1. Vẽ một tam giác vuông và các hình vuông trên các cạnh của nó (dùng công cụ custom)2. Kéo dài tia HA, lấy điểm A’ đối xứng với điểm H qua A bằng cách :+ Chọn đoạn HA và điểm A+ Chọn menu Transform --> Rotate --> degrees =1803. Vẽ một đường thẳng đi qua điểm B và vuông góc với đoạn AA’, Vẽ điểm giao K của 2 đường này.( Hình bên minh họa cho các bước từ 1 đến 3)4. Vẽ hình vuông A’KLM.(Sử dụng công cụ Custom tool như đã giới thiệu ở bài 1)5. Vẽ Đoạn BK, GM, FL.6. Làm ẩn đi đường BK.7. Tô màu cho 4 mảnh trong hình vuông trên cạnh huyền.8. Đánh dấu vectơ EJ và dịch chuyển 4 đỉnh và 4 cạnh của hình vuông BCDE theo vectơ này (để được hình vuông bên dưới hình vuông trên cạnh b có diện tích bằng diện tích hình vuông BCDE )+ Đánh dấu theo thứ tự điểm E, J+ Chọn menu Transform --> Mark vector+ Đánh dấu 4 cạnh và 4 đỉnh của hình vuông BCDE+ Chọn vào Menu Transform --> Translate

Xem nội dung đầy đủ tại:http://123doc.org/document/542584-mot-so-cach-chung-minh-dinh-ly-pitago.htm

Có 6 cách nè:
Cách 1+cách 2:có trong SGK toán 7(PP diện tích)
Cách 3:(của một Tổng thống Mỹ hẳn hoi,ko biết có đúng ko)
Cho 2 tam giác vuông ABC và A'BC' (góc A= góc A' =90 độ)đặt cạnh nhau sao cho có được hình thang vuông ACC'A'(AC song song A'C') rồi dùng Đại số là ra
Cách 4:(của một nhà toán học Ấn Độ)
Dựng hình vuông ABCD và các tam giác vuông MAB,NBC,PCD,QDA để được hình vuông MNPQ rồi lại Đại số là ra
Cách 5:(thuần túy Hình học)Với ABC(góc A=90 độ) dựng ra ngoài 3 hình vuông ABDE,ACGH và BCM rồi dùng tam giác bằng nhau
Cách 6:Sử dụng hệ thức lượng trong tam giác vuông(lớp 9) 

? đề bài 

lag!!!! :D

mik ko hiểu đề bài nha

hok tốt

Việt