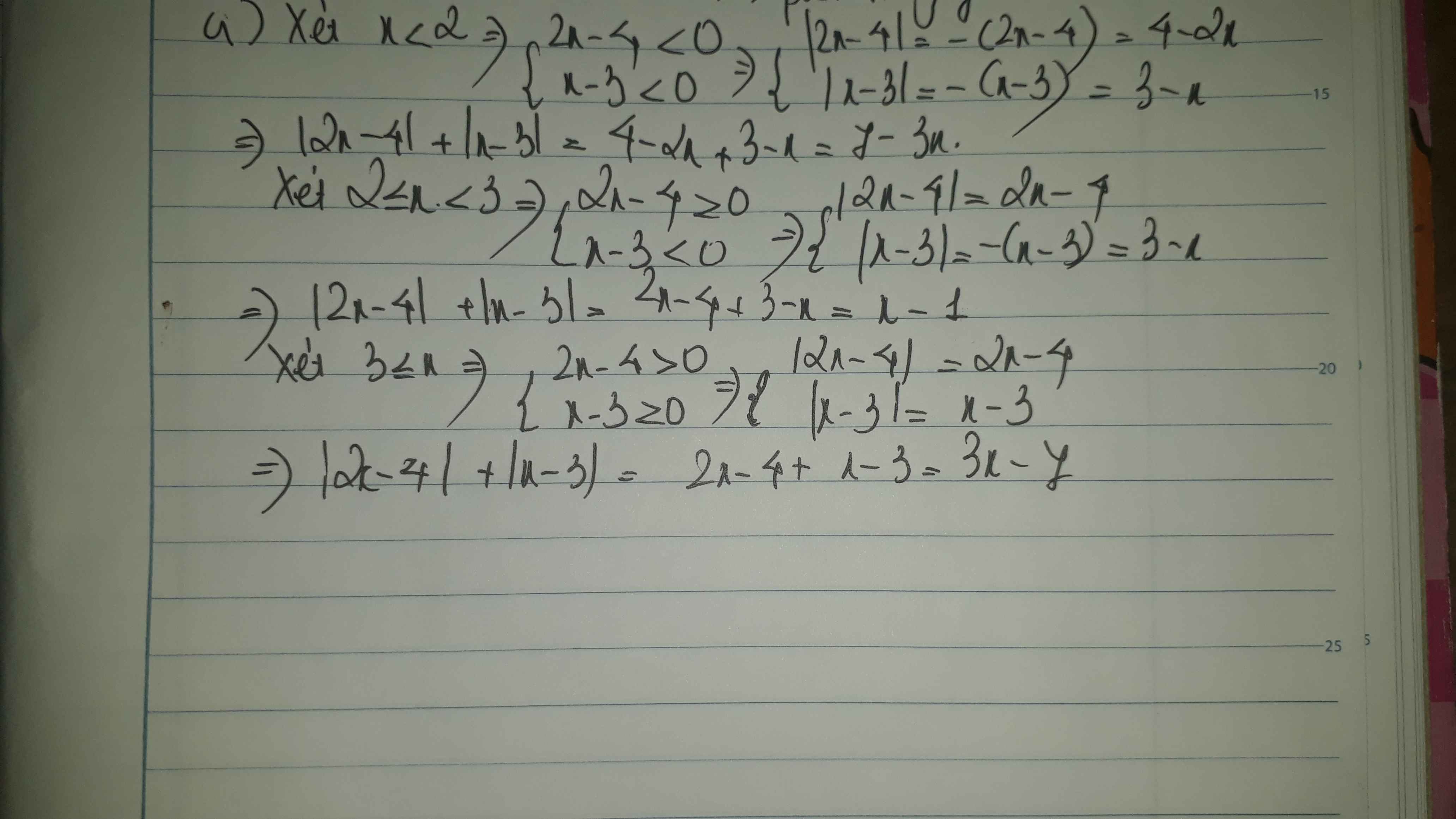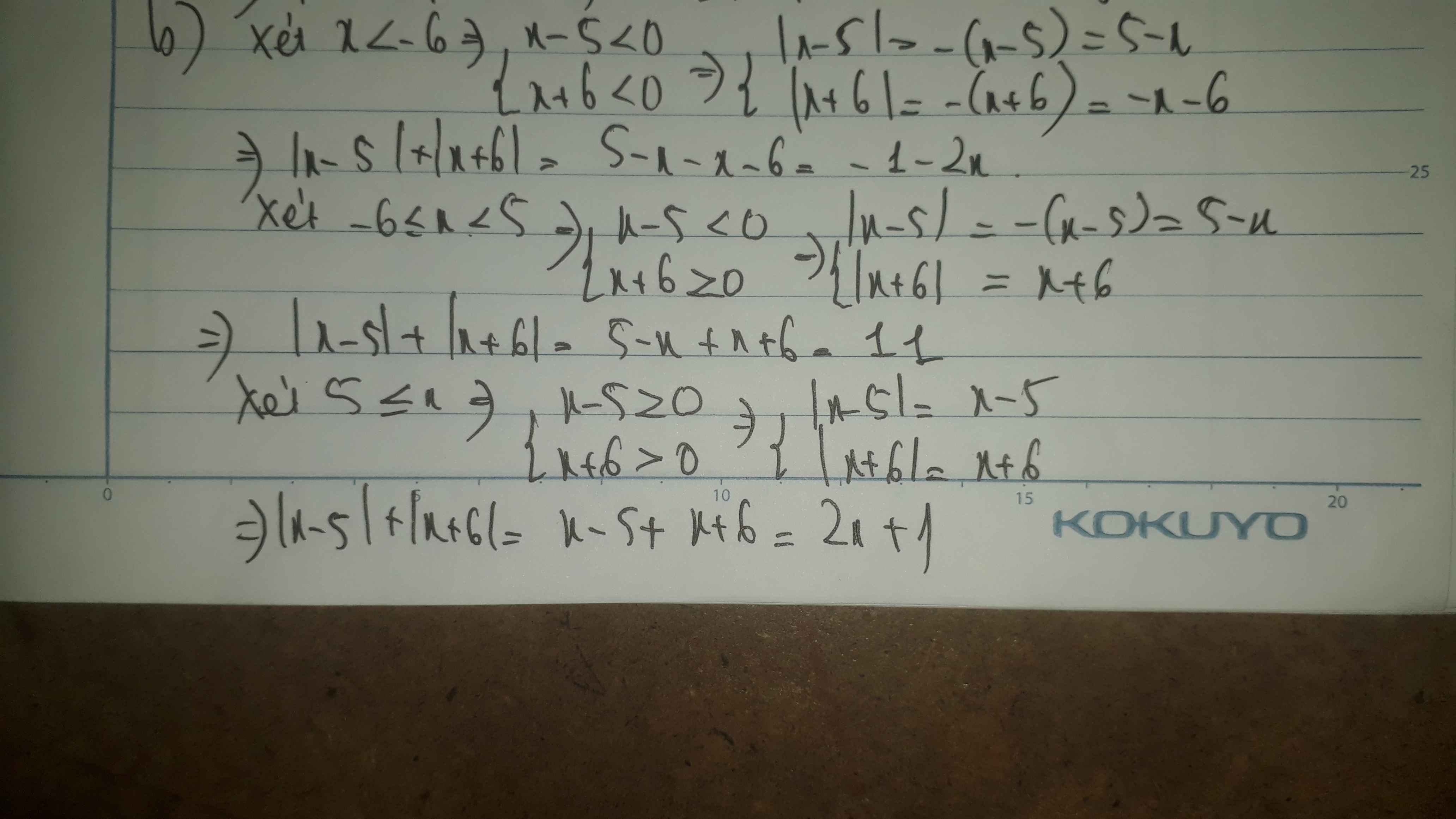Cho x thuộc Z , hãy bỏ dấu giá trị tuyệt đối rồi rút gọn biểu thức M= |x-3| + x - 5 với x < 3

Những câu hỏi liên quan
Cho x thuộc Z , hãy bỏ dấu giá trị tuyệt đối rồi rút gọn biểu thức N = |2 + x| - ( x + 1 ) với x lớn hơn hoặc bằng -2
N=\(\left|2+x\right|-\left(x+1\right)=2+x-x-1=1\) (vì \(x\ge-2\Rightarrow\left|2+x\right|=2+x\))
Đúng 0
Bình luận (0)
hãy bỏ dấu giá trị tuyệt đối rồi rút gọn các biểu thức sau :
a, |x-3| + x - 5 với x < 3
a, |x-3| + x - 5 ( x < 3 )
với x < 3 , | x - 3 | + x - 5
= -(x-3) + x - 5 = -2
hok tốt
Đúng 0
Bình luận (0)
a) \(|x-3|+x-5\) với \(x< 3\)
\(\Rightarrow x-3+x-5\)với \(x< 3\)
\(\Rightarrow x=5-3\)
\(\Rightarrow x=2\)
Vì \(x< 3\)nên \(x=2\)
Vậy \(x=2< 3\)
Hk tốt,
k nhé
Đúng 0
Bình luận (0)
| x - 3 | + x - 5 ( với x < 3 )
với x < 3 , ta có :
x - 3 + x - 5 với x < 3
x - x = 3 - 5
x = -2
Đúng 0
Bình luận (0)
Cho x thuộc Z. Hayz bỏ dấu giá trị tuyệt đối rồi rút gọn các biểu thức sau:
a) |x - 5| + x - 10 với x < 5
b) |7 + x | - (x - 8) với ≥ -7
c) |x + 3| + |x - 4| với -3 ≤ x ≤ 4.
b) x \(\ge-7\Leftrightarrow\)7+x|=7+x ⇔B=|7+x|−(x−8)=7+x−x+8=15
c)|x+3|+|x−4| TH1: x≤−3 <=> |x+3|+|x−4|=−x−3+4−x=1−2x
TH2: −3<x≤4 <=> |x+3|+|x−4|=x+3+4−x=7
TH3: x > 4 <=>|x+3|+|x−4|=x+3+x-4=2x-1
Đúng 0
Bình luận (0)
bỏ dấu giá trị tuyệt đối rồi rút gọn các biểu thức sau:a,|2x-4|+|x-3|;b, |x-5|+|x+6|
a. \(\left|2x-4\right|+\left|x-3\right|\)
Với \(x< 2\), biểu thức trở thành
\(-\left(2x-4\right)-\left(x-3\right)\)
\(=-2x+4-x+3\)
\(=-3x+7\)
Với \(2\le x< 3\), biểu thức trở thành
\(\left(2x-4\right)-\left(x-3\right)\)
\(=2x-4-x+3\)
\(=x-1\)
Với \(x\ge3\), biểu thức trở thành
\(\left(2x-4\right)+\left(x-3\right)\)
\(=2x-4+x-3\)
\(=3x-7\)
b. \(\left|x-5\right|+\left|x+6\right|\)
Với \(x< -6\), biểu thức trở thành
\(-\left(x-5\right)-\left(x+6\right)\)
\(=-x+5-x-6\)
\(=-2x-1\)
Với \(-6\le x< 5\), biểu thức trở thành
\(-\left(x-5\right)+\left(x+6\right)\)
\(=-x+5+x+6\)
\(=11\)
Với \(x\ge5\), biểu thức trở thành
\(\left(x-5\right)+\left(x+6\right)\)
\(=x-5+x+6\)
\(=2x+1\)
Đúng 0
Bình luận (0)
Hãy bỏ dấu giá trị tuyệt đối rồi rút gọn các biểu thức sau :
!2 + x ! - ( x + 1 ) với x > -2
ta có x> -2
=>2+x >0
=>/2+x/=2+x
=> /2+x/-(x+1)=2+x -x-1=1
Hok tốt
Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức sau: A = | x - 1 | + 3 - x khi x ≥ 1.
Khi x ≥ 1 ta có x - 1 ≥ 0 nên | x - 1 | = x - 1
Do đó A = | x - 1 | + 3 - x = x - 1 + 3 - x = 2.
Đúng 0
Bình luận (0)
Cho x \(\in\)Z , hãy bỏ dấu giá trị tuyệt đối rồi rút gọn các biểu thức sau
a, B = | 7 + x | - ( x - 8 ) với x \(\ge\) - 7
b, C = | x + 3 | + | x - 4 |
Các bn giúp mik nhe , chiều nay mik phải nộp bài rùi
a)\(x\ge-7\Leftrightarrow\left|7+x\right|=7+x\)
\(\Leftrightarrow B=\left|7+x\right|-\left(x-8\right)=7+x-x+8=15\)
b)\(C=\left|x+3\right|+\left|x-4\right|\)
TH1: \(x\le-3\)
<=>\(C=\left|x+3\right|+\left|x-4\right|=-x-3+4-x=1-2x\)
TH2: \(-3< x\le4\)
<=>\(C=\left|x+3\right|+\left|x-4\right|=x+3+4-x=7\)
TH3: x > 4
<=>\(C=\left|x+3\right|+\left|x-4\right|=x+3+x-4=2x-1\)
Đúng 0
Bình luận (0)
toán buổi chiều hay nha cô dương đúng ko?
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức: C = |x - 4| - 2x + 12 khi x > 5
- Khi x > 5 ta có x - 4 > 1 (trừ hai vế cho 4) hay x - 4 > 0 nên |x - 4| = x - 4
Vậy C = x - 4 - 2x + 12 = -x + 8
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau: A = | x - 4 | - x + 1 với x < 4
Ta có: x < 4 ⇒ | x - 4 | = 4 - x
Khi đó ta có: A = | x - 4 | - x + 1 = 4 - x - x + 1 = 5 - 2x.
Vậy A = 5 - 2x
Đúng 0
Bình luận (0)