Tìm 2 chữ số a và b biết: 2ab=b0,a+b,a

Những câu hỏi liên quan
Cho hai số thực không âm \(a\) và \(b\), biết \(a^2+b^2=6\). Tìm giá trị lớn nhất của biểu thức \(P=\dfrac{2ab}{a+b+2}\)
Biết các số thực a,b thỏa mãn:
0
b
a
≤
2
và
2
a
b
≤
2
b
+
a
Tìm giá trị lớn nhất của F
a
2
+
b
2
Đọc tiếp
Biết các số thực a,b thỏa mãn: 0 < b < a ≤ 2 và 2 a b ≤ 2 b + a Tìm giá trị lớn nhất của F= a 2 + b 2
![]()
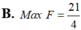
![]()
![]()
tìm ab biết a^2+b^2=32 và a+2ab+b=40
\(\left\{{}\begin{matrix}a^2+b^2=32\\a+b+2ab=40\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2+2ab+a+b=72\\a+b+2ab=40\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a+b\right)^2+\left(a+b\right)-72=0\\a+b+2ab=40\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a+b=8\\a+b=-9\end{matrix}\right.\\a+b+2ab=40\end{matrix}\right.\)
TH1: \(a+b=8\Rightarrow ab=16\)
\(\Rightarrow a\left(8-a\right)=16\Leftrightarrow a^2-8a+16=0\)
\(\Leftrightarrow\left(a-4\right)^2=0\Rightarrow a=4\Rightarrow b=4\)
TH2: \(a+b=-9\Rightarrow ab=\dfrac{49}{2}\)
\(\Rightarrow a\left(-9-a\right)=\dfrac{49}{2}\) \(\Leftrightarrow2a^2+18a+49=0\)
\(\Leftrightarrow2\left(a+\dfrac{9}{2}\right)^2+\dfrac{17}{2}=0\) (ko tồn tại a thỏa mãn)
Vậy \(\left\{{}\begin{matrix}a=4\\b=4\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cách 2:
Với mọi số thực a; b ta luôn có:
\(\left(a-4\right)^2+8\left(a-b\right)^2+\left(b-4\right)^2\ge0\)
\(\Leftrightarrow a^2-8a+16+8\left(a^2-2ab+b^2\right)+b^2-8a+16\ge0\)
\(\Leftrightarrow9\left(a^2+b^2\right)\ge8\left(a+b+2ab\right)-32\)
\(\Leftrightarrow9\left(a^2+b^2\right)\ge288\)
\(\Leftrightarrow a^2+b^2\ge32\)
Đẳng thức xảy ra khi và chỉ khi \(a=b=4\)
Đúng 2
Bình luận (0)
Cộng hai vế của hai phương trình trên có :
\(a^2+b^2+2ab+a+b=72\)
\(\Leftrightarrow\left(a+b\right)^2+a+b-72=0\)
\(\Leftrightarrow\left(a+b-8\right)\left(a+b+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=8\\a+b=-9\end{matrix}\right.\)
+) Với \(a+b=8\Rightarrow2ab=40-a-b=40-8=32\) \(\Rightarrow ab=16\)
+) Với \(a+b=-9\Rightarrow ab=\dfrac{49}{2}\)
Đúng 0
Bình luận (0)
tìm các chữ số a,b biết:
ab2 + 512 =3 x 2ab
biết a<b<0 và a,b thỏa mãn: a(a+2)+b(b-2)-2ab=63 tìm a,b
tìm tất cả các chữ số a,b biết \(2ab^-+1\)và \(3ab^-+1\)đều là các số chính phương
Tìm các chữ số a,b biết 2ab +1 và 3ab +1 đều là số chính phương
Tìm 2 STN a và b ( a< b0 a+b=72 và BCNN (a;b) = 42
Tìm a,b thuộc Z biết:
a)2ab-b+3a=10
b)a2-2ab+4a-8b=7














