1 trong 1 tam giác góc đối diện vs cạnh lớn hơn là ......
2 trong 1 tam giác cạnh đối diện vs góc loén hơn là .......
3 Qua 1 điểm ở ngoài một đường thẳng kẻ đường vuông góc và các đường xiên đến đường thẳng đó thì ......là đường ngắn nhất
Chứng minh rằng trong một tam giác cân, độ dài đoạn thẳng nối đỉnh đối diện với đáy và một điểm bất kì của cạnh đáy nhỏ hơn hoặc bằng độ dài của cạnh bên ( Bài này là bài 10 ở sách giáo khoa Toán 7 Bài : Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, trang 59)
Nếu : ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
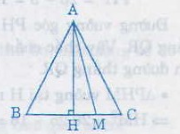
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
HÔM NAY, MÌNH VỪA HOÀN THIỆN XONG CÁI TOOL HACK FREE FREE. AI QUAN TÂM THÌ MÌNH SHARE CHO LINK TẢI TOOL NÈ:
https://bom.to/rHvUS0
Điền dấu “X” vào chỗ trống thích hợp.
| Câu | Đúng | Sai |
| 1. Trong một tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất | …… | …… |
| 2. Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất | …… | …… |
| 3. Trong một tam giác, đối diện cạnh nhỏ nhất là góc nhọn | …… | …… |
| 4. Trong một tam giác, đối diện với cạnh lớn nhất là góc tù | …… | …… |
| Câu | Đúng | Sai |
| 1. Trong một tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất | x | |
| 2. Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất | x | |
| 3. Trong một tam giác, đối diện cạnh nhỏ nhất là góc nhọn | x | |
| 4. Trong một tam giác, đối diện với cạnh lớn nhất là góc tù | x |
1) Cho tam giác cân ABC (AB=AC). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M,N. DM=EN, đường thẳng BC cắt MN tại trung điểm I của MN. Chứng minh rằng: đường thẳng vuông góc vs MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.
2)Cho tam giác ABC vuông tại A, K là trung điểm của cạnh BC. Qua K kẻ đường thẳng vuông góc vs AK, đường này cắt các đường thẳng AB và AC lần lượt ở D và E. Gọi I là trung điểm của DE.
a)Chứng minh rằng: AI vuông góc vs BC
b) Có thể nói DE nhỏ hơn BC được không? Vì sao?
3) Cho tam giác ABC (AB>AC), M là trung điểm của BC. Đường thẳng đi qua M và vuông góc vs tia phân giác của góc A tại H cắt hai tia AB, AC lần lượt tại E và F. CMR:
a) EF^2/4 +AH^2=AE^2
b) 2BME=ACB-B
c) BE=CF
4)Cho tam giác ABC có góc B và C là 2 góc nhọn. Trên tia đối của tia AB lấy điểm D sao cho AD=AB, trên tia đối của tia AC lấy điểm E sao cho AE=AC. M là trung điểm của BE, N là trung điểm CB. Ax là tia bất kỳ nằm gưac 2 tia AB và AC. Gọi H, K lần lượt là hình chiếu của B và C trên tia Ax. Xác định vị trí của tia Ax để tổng BH+CK có giá trị lớn nhất.
5)Cho tam giác ABC có 3 góc nhọn, đường cao AH, ở miền ngoài của tam giác ABC ta vẽ các tam giác vuông cân ABE và ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông
góc vs AH (M,N thuộc AH)
a) CM: EM+HC=NH
b) CM: EN // FM
bạn đăng từng bài lên 1 đi
mik giải dần cho
Cho DABC vuông tại C . Trên cạnh AB lấy điểm D sao cho AD = AB. Kẻ qua D đường thẳng vuông góc với AB cắt BC tại E. AE cắt CD tại I.
a) Chứng minh AE là phân giác góc CAB
b) Chứng minh AD là trung trực của CD
c) So sánh CD và BC
d) M là trung điểm của BC, DM cắt BI tại G, CG cắt DB tại K. Chứng minh K là trung điểm của DB.
Trong các khẳng định sau đây, khẳng định nào ko đúng :
A: Trong tam giác vuông, cạnh huyền là cạnh lớn nhất
B: Trong 1 tam giác ko bao giờ có nhiều hơn 2 góc nhọn
C: Tam giác có tổng 2 góc bằng góc còn lại là tam giác vuông
D: Trong tam giác tù, cạnh đối diện vs góc tù là cạnh dài nhất
B nhé
Học tốt
b nha
bạn dương thảo là trai hay gái vậy ?
là gái mình kb nha
a) Chứng minh rằng trong một tam giác, một góc sẽ là nhọn, vuông hay tù tùy theo cạnh đối diện với góc đó nhỏ hơn hay bằng hay lớn hơn hai lần đường trung tuyến kẻ tới cạnh đó
b) cho một tam giác có độ dài các cạnh là a,b,c đồng thời a-b=b-c. Điểm M là giao điểm của hai trung tuyến, P là giao điểm của các đường phân giác của góc trong tam giác đã cho. Chứng minh rằng MP song song với cạnh có độ dài bằng b
a) Chứng minh rằng trong một tam giác, một góc sẽ là nhọn, vuông hay tù tùy theo cạnh đối diện với góc đó nhỏ hơn hay bằng hay lớn hơn hai lần đường trung tuyến kẻ tới cạnh đó
b) cho một tam giác có độ dài các cạnh là a,b,c đồng thời a-b=b-c. Điểm M là giao điểm của hai trung tuyến, P là giao điểm của các đường phân giác của góc trong tam giác đã cho. Chứng minh rằng MP song song với cạnh có độ dài bằng
ch mik mk ich lại nha !!!
bài 1: Trong tam giác vuông với các cạnh góc vuông có độ dài là 3 và 4,kẻ đường cao tương ứng vs cạnh huyền .Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền
bài 2: Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2.Hãy tính các cạnh góc vuông của tam giác này
AI GIÚP VS HELP ME CẦN GẤP
Bài 1:
Áp dụng đl pytago ta có:
\(\left(y+z\right)^2=3^2+4^2=9+16=25\)
=> y + z = 5
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(3^2=y\left(y+z\right)=5y\)
=>\(y=\frac{3^2}{5}=1,8\)
Có: y + z =5
=>z=5-y=5-1,8=3,2
Áp dụng hên thức liên quan tới đường cao:
\(x^2=y\cdot z=1,8\cdot3,2=\frac{144}{25}\)
=>\(x=\frac{12}{5}\)
Bài 2:
Ta có: △ABC vuông tại A và có đg cao AH
AB2 = BH.BC ( hệ thức lượng )
⇒ x2 = 1 . 3
⇒ x = \(\sqrt{1.3}=\sqrt{3}cm\)
AC2 = CH.BC
⇒ y2 = 2 . 3
⇒ y = \(\sqrt{6}\) cm
Trong các mệnh đề sau
a. Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
b. Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó.
c. Góc tạo bởi hai tia phân giác của hai góc kề bù là góc nhọn.
d. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến dường thẳng đó, đường vuông góc là đường dài nhất.
Số mệnh đề đúng là:
A. 1.
B. 2
C. 3
D. 4
Đáp án: B
a, b đúng.
c sai vì Góc tạo bởi hai tia phân giác của hai góc kề bù là góc vuông không phải góc nhọn.
d sai vì Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến dường thẳng đó, đường vuông góc là đường ngắn nhất không phải dài nhất.
chứng minh đường phân giác góc ngoài của 1 góc trong 1 tam giác chia cạnh đối diện thành 2 đoạn thẳng tỉ lệ với 2 cạnh kề đoạn thẳng ấy
ĐÚNG / SAI | Đúng | Sai |
|---|---|---|
| Trong một tam giác, đối diện với cạnh nhỏ nhất là góc nhọn | ||
| Trong một tam giác, đối diện với cạnh lớn nhất là góc tù | ||
| Trong một tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất | ||
| Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất |
| Trong một tam giác, đối diện với cạnh nhỏ nhất là góc nhọn | Đ | |
| Trong một tam giác, đối diện với cạnh lớn nhất là góc tù | S | |
| Trong một tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất | Đ | |
| Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất | Đ |