Xét biểu thức f(x)=\(\frac{X^2+3x-10}{x^2-1}\)

Những câu hỏi liên quan
Bài 3: Xét dấu các biểu thức sau 1/ f(x) = (2x - 1)(x ^ 3 - 1)
. 2 / (f(x)) = (- 2x ^ 2 + 7x + 7)/(x ^ 2 - 3x - 10) - 1
Xét dấu các biểu thức sau:
a) f(x)= (x-2).(x+1)/3x -1
b) f(x)= 1-4x /2x-3
c) f(x)= 3x (6 -2x)/5x-4
d) f(x)= -4/3x+1 - 3/2-x
e) f(x)= 2x-5/(3x+1) (2-4x)
Xem chi tiết
Xét các dấu biểu thức : a) f(x) = (3-x)(x+2) b) f(x) = (x-1)(x^2-6x-7) c) f(x) = -3x^2 + x + 2
xét dấu biểu thức f(x)=\(\frac{x^2+3x-10}{x^2-1}\)
\(f\left( x \right) = \dfrac{{{x^2} + 3x - 10}}{{{x^2} - 1}} = \dfrac{{\left( {x + 5} \right)\left( {x - 2} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)
Cho \(f(x)=0 \Rightarrow x=-5;x=2;x=1;x=-1\)
Bảng xét dấu:

\(f(x > 0\) khi \(x<-5\)\(;-1< x< 1;x>2\)
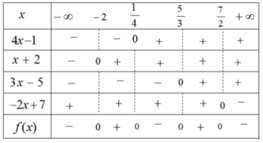
Xét dấu biểu thức sau: f(x) = (4x - 1)(x + 2)(3x - 5)(-2x + 7)
f(x)=(3x+1)/(x+1)-(4)/(x^(2)-2x+1)
Xét dấu biểu thức ạ ai giúp mình với
Xét dấu biểu thức: f(x) = (-3x - 3)(x + 2)(x + 3)
Nhị thức –3x – 3 có nghiệm là –1; nhị thức x + 2 có nghiệm là –2 ; nhị thức x + 3 có nghiệm là –3.
Ta có bảng xét dấu :

Kết luận :
+ f(x) < 0 khi –3 < x < –2 hoặc x > –1
+ f(x) > 0 khi x < –3 hoặc –2 < x < –1.
+ f(x) = 0 khi x = –3 hoặc x = –2 hoặc x = –1.
Đúng 0
Bình luận (0)
Bài 1. Xét dấu các biểu thức sau:
1. \(f\left(x\right)=\left(x-2\right)\left(5-3x\right)\left(x^2-x+3\right)\left(x^2+2x+1\right)\left(x^2-5x+4\right)\)
2. \(g\left(x\right)=\frac{5}{1-x}+\frac{5x}{x+1}+\frac{1}{x^2-1}\)
Xét dấu các biểu thức tích, thương các tam thức bậc hai
a. \(f\left(x\right)=x^2\left(2-x-x^2\right)\left(x+2\right)\)
b. \(f\left(x\right)=\frac{x^4-3x^3+2x^2}{x^2-x-30}\)
a) F(x) = \(-x^2\left(x-1\right)\left(x+2\right)\left(x+2\right)=\left(1-x\right)x^2\left(x+2\right)^2\\ \)
\(\left\{{}\begin{matrix}x^2\ge0\\\left(x+2\right)^2\ge0\end{matrix}\right.\) => dấu biểu thức chỉ phụ thuộc vào thừa số (1-x)
F(x) =0 khi x={-2,0,1}
F(x) > 0 khi x<1 và khác -2 và 0
f(x) <0 khi x> 1
Đúng 0
Bình luận (0)
Tử f(x) =x^2(x^2-3x+2) =x^2(x-1)(x-2)
tương tự a) dấu của tử phụ thuộc (x-1)(x-2)
Mẫu f(x) =x^2 -x-30 =(x-5)(x+6)
Phần hỗ trợ Lập bảng đây khó thao tác
=> viết bằng hệ {điểm tới hạn xet x={-6,0,1,2,5}
Khi => \(\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)=>f(x) =0
Khi \(\left[{}\begin{matrix}x=5\\x=-6\end{matrix}\right.\) => f(x) không xác định
Khi \(x< -6\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)>0\end{matrix}\right.\)\(\Rightarrow f\left(x\right)>0\)
khi -6<x<1 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) <0
khi 1<x<2 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)< 0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) >0
khi 2<x<5 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) <0
khi x>5 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)>0\end{matrix}\right.\) => f(x) >0
Đúng 0
Bình luận (0)