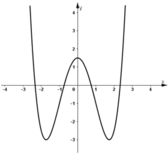
khảo sát sự biến thiên và vẽ đồ thị hàm số:
a. y=x3-3x2+2
b. y=x3+1
Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x 3 + 3 x 2 + 1

+ Bảng biến thiên:
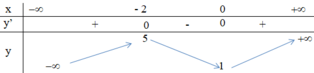
Kết luận:
Hàm số đồng biến trên các khoảng (-∞; -2) và (0; +∞).
Hàm số nghịch biến trên khoảng (-2; 0).
Hàm số đạt cực tiểu tại x = 0 ; y C T = 1 .
Hàm số đạt cực đại tại x = -2 ; y C Đ = 5 .
- Đồ thị:
+ Giao với Oy: (0; 1).
+ Đồ thị (C) đi qua điểm (–3; 1), (1; 5).
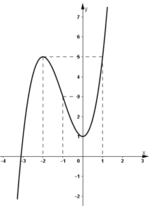
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: f x = - x 3 + 3 x 2 + 9 x + 2
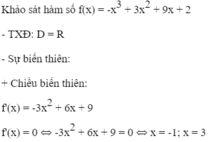
+ Giới hạn:
+ Bảng biến thiên:
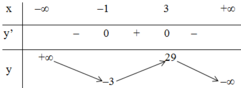
Kết luận:
Hàm số đồng biến trên (-1; 3)
Hàm số nghịch biến trên (-∞; -1) và (3; +∞).
Hàm số đạt cực đại tại x = 3, yCĐ = 29.
Hàm số đạt cực tiểu tại x = -1; y C T = - 3
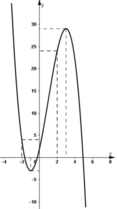
- Đồ thị:
+ Giao với trục tung tại (0; 2).
+ Đi qua các điểm (-2; 4); (2; 24).
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a. y=x3-3x+2
b. y=x3+1
c. y= -x3+3x+1
d. y=-x3-5x2-9x-4
e. y=x4-2x2-1
f. y= \(-\dfrac{x^4}{2}\)-x2+\(\dfrac{3}{2}\)
g. y=2x2-x4
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y = − x 3 + 3x + 1
Cho hàm số : y = x 3 – 3 x 2 . Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
TXĐ: D = R
Sự biến thiên:
y′ = 3 x 2 – 6x = 3x(x – 2)
y′=0 ⇔ 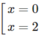
Hàm số đồng biến trên mỗi khoảng (– ∞ ;0), (2;+ ∞ )
Hàm số nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0 ; y CĐ = y(0) = 0
Hàm số đạt cực tiểu tại x = 2; y CT = y(2) = -4.
Giới hạn: 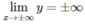
Điểm uốn: y” = 6x – 6, y” = 0 ⇔ x = 1; y(1) = –2
Suy ra đồ thị có điểm uốn I(1; -2)
Bảng biến thiên:
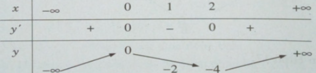
Đồ thị:
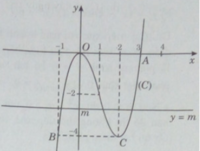
Đồ thị cắt trục hoành tại O(0;0), A(3;0). Đồ thị đi qua điểm B(-1;-4); C(2;-4).
Khảo sát sự biến thiên và vẽ đồ thị hàm số:
a) y= x4+2x2-3
b) y= -x4-4x-1
Cho hàm số: y = 4 x 3 + mx (m là tham số) (1). Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1
y = 4 x 3 + x, y′ = 12 x 2 + 1 > 0, ∀ x ∈ R
Bảng biến thiên:
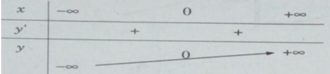
Đồ thị:
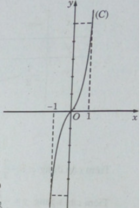
Cho hàm số y = x 3 + a x 2 + bx+1
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với các giá trị tìm được của a và b
Với a = 1; b = -1, hàm số trở thành: y = x 3 + x 2 – x + 1.
- Tập xác định : D = R.
- Sự biến thiên :
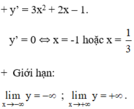
+ Bảng biến thiên :
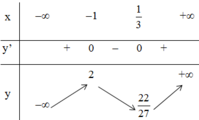
Kết luận :
Hàm số đồng biến trên (-∞ ; -1) và 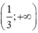
Hàm số nghịch biến trên 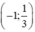
Hàm số đạt cực đại tại x = -1 ; yCĐ = 2.
Hàm số đạt cực tiểu tại 
- Đồ thị :
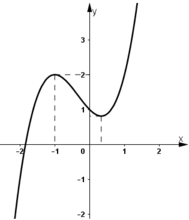
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y = 1 2 x 4 - 3 x 2 + 3 2
Khảo sát hàm số y = 1 2 x 4 - 3 x 2 + 3 2
- TXĐ: D = R
- Sự biến thiên:
+ Chiều biến thiên:
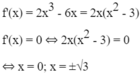
+ Giới hạn tại vô cực:
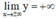
+ Bảng biến thiên:
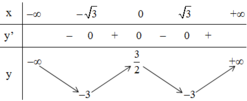

Hàm số đạt cực đại tại x = 0, yCĐ = 3 2
Hàm số đạt cực tiểu tại x = 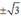 ; yCT = -3.
; yCT = -3.
- Đồ thị:
+ Đồ thị hàm số nhận trục tung là trục đối xứng.
+ Đồ thị cắt trục tung tại (0; 1,5).