Trên cùng một nửa phẳng có bờ chứa tia Ox, vẽ các góc xOy=40; xOz=120
a, Tính số đo góc yOz
b, vẽ tia Ot là phân giác góc xOz. Tính số đo góc tOy
c, gọi om là tia đối. Tính góc xOm
Cho góc nhọn xOy. Trên một nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia Ox' vuông góc với Ox. Trên một nửa mặt phẳng bờ Oy chứa tia Ox vẽ tia Oy' vuông góc với Oy. CMR hai góc xOy và x'Oy' có cùng tia phân giác và tổng hai góc bằng 180 độ.
Các bn nhớ vẽ hình nha
Cho góc xOy là góc tù. Trên nửa mặt phẳng chứa tia Ox có bờ chứa tia Oy, vẽ tia Oy' vuông góc với Oy. Trên nửa mặt phẳng chứa tia Oy có bờ chứa tia Ox vẽ Ox' vuông góc với Ox
a) Chứng minh góc xOy'=x'Oy'
b) Góc xOy và góc xOy'có cùng một tia phân giác
Cho góc xOy là góc tù. Trên nửa mặt phẳng chứa tia Ox có bờ chứa tia Oy, vẽ tia Oy' vuông góc với Oy. Trên nửa mặt phẳng chứa tia Oy có bờ chứa tia Ox vẽ Õ' vuông góc với Ox
a) Chứng minh góc xOy'=x'Oy'
b) Góc xOy và góc xOy'có cùng một tia phân giác
Cho góc nhọn xOy. Trên nửa mặt phẳng chứa tia Oy, bờ chứa tia Ox, vẽ góc vuông xOa. Trên nửa mặt phẳng chứa tia Ox, bờ chứa tia Oy, vẽ góc vuông yOb.
a)Chứng minh góc aOb là góc tù
b) Chứng minh các góc xOy và sOb có cùng một tia phân giác
Trên cùng một nửa mặt phẳng bờ chứa tia Ox. Vẽ các tia Oy, Oz sao cho góc xOy=40 độ, góc xOz=80 độ.
a. Tia Oy có phải là tia phân giác của góc xOz không?
b. Vx tia Ot sao cho tia Ot, Oy cùng thuộc một nửa mặt phẳng có bờ chứa tia Ox và xOt=3/2 góc xOy.Tính góc yOt
sorry mk ko vẽ đc hình
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox có xÔy < xÔz ( 40 * < 80* )
nên tia Oy nằm giữa 2 tia Ox và Oz
suy ra xÔz + yÔz = xÔz
40* + yÔz = 80*
yÔz = 80* - 40 * = 40*
- Tia Oy là tia phân giác của xÔz vì
+ tia Oy nằm giữa 2 tia Ox và Oz
+ xÔy = yÔz = 40*
b) vì tia Ot là tia đối của tia Ox nên tÔx = 180*
Cho góc nhọn x O y ^ . Trên một nửa mặt phẳng bờ Ox chứa tia Oy, kẻ tia Ox' vuông góc với Ox. Trên một nửa mặt phẳng bờ Oy chứa tia Ox, vẽ tia Oy' vuông góc với Oy. Chứng minh hai góc x O y ^ và x ' O y ' ^ có cùng tia phân giác và tổng số đo hai góc bằng 180°.
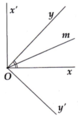
Ta có: x O y ^ + x ' O y ^ = 90° và x O y ^ + x O y ' ^ = 90° => x ' O y ^ = x O y ' ^ .
Mặt khác Ox', Oy' nằm trên hai nửa mặt phẳng đối nhau bờ Ox nên Ox nằm giữa hai tia Ox' và Oy'.
Tương tự Oy nằm giữa hai tia Ox' và Oy'
Gọi Om là phân giác góc xOy, suy ra Oy
nằm giữa Ox' và Om, Ox nằm giữa Oy' và
Om, Om nằm giữa Ox và Oy.
Lại có Om là phân giác góc xOy
=> x O m ^ = y O m ^ và x ' O y ^ = x O y ' ^ (cùng phụ x O y ^ ). Do đó x ' O m ^ = y ' O m ^ .
=> Om cũng là phân giác của x ' O y ' ^ (ĐPCM)
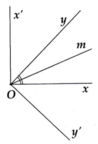
Cho góc nhọn x O y ^ . Trên một nửa mặt phẳng bờ Ox chứa tia Oy, kẻ tia Ox' vuông góc với Ox. Trên một nửa mặt phẳng bờ Oy chứa tia Ox, vẽ tia Oy' vuông góc với Oy. Chứng minh hai góc x O y ^ và x ' O y ' ^ có cùng tia phân giác và tổng số đo hai góc bằng 180 ° .
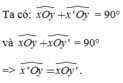
Mặt khác Ox', Oy' nằm trên hai nửa mặt phẳng đối nhau bờ Ox nên Ox nằm giữa hai tia Ox' và Oy'.
Tương tự Oy nằm giữa hai tia Ox' và Oy'
Gọi Om là phân giác góc xOy, suy ra Oy nằm giữa Ox' và Om, Ox nằm giữa Oy' và Om, Om nằm giữa Ox và Oy.

Cho xOy là góc tù. Trên nửa mặt phẳng chứa tia Ox có bờ chứa tia Oy, vẽ tia Oý vuông góc Oy, trên nửa mặt phẳng chứa tia Oy có bờ chứa tia Ox. Vẽ Ox’ vuông góc Ox. Chứng minh rằng: a, xOy’ = x’Oy
b, 2 góc xOy và x’Oy’ có cùng tia phân giác
c, 2 góc xOy và x’Oy’ bù nhau
a) Ta có :
xOy' + y'Ox' =90 độ (gt)
y'Ox' + x'Oy = 90 độ (gt)
=> xOy' = 90 - y'Ox'
=> x'Oy = 90 - y'Ox'
=> xOy' = x'Oy (cùng bằng 90 - y'Ox')(dpcm)
b) Gọi Ot là pg y'Ox'(1)
=> y'Ot = x'Ot
tOy = tOx' + x'Oy
Mà y'Ot = tOx'
xOy' = x'Oy (cmt)
=> xOt = tOy
=> Ot là pg xOy (2)
Từ (1) và (2) ta có :
=> y'Ox' và xOy có cùng tia pg
Trên cùng một nửa mặt phẳng bờ chứa tia Ox. Vẽ hai tia Ox và Oz sao cho góc xOy= 40 độ,góc xOz=120 độ
a.) Tính góc yOz?
b.) Trên cùng một nửa mătj phẳng bờ Oz chứa tia Oy vẽ góc zOm=60 độ. Gọi Ox' là tia đối của tia Ox. Chứng tỏ tia Oz là tia phân giác của x'Om
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ tia Oy, Oz sao cho góc xOy = 40 độ; xOz = 110 độ. Vẽ các tia phân giác Om, On của xOy và yOz. Tính góc mOn.
Giải
Trên cùng một nửa mặt phẳng bờ chứa tia Ox có \(\widehat{xOy}< \widehat{xOz}\left(40^0< 110^0\right)\)
\(\Rightarrow\)Tia Oy nằm giữa hai tia Ox và Oz.
\(\Rightarrow\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
hay \(40^0+\widehat{yOz}=110^0\)
\(\Leftrightarrow\widehat{yOz}=110^0-40^0\)
\(\Leftrightarrow\widehat{yOz}=70^0\)
Vì Om là tia phân giác của \(\widehat{xOy}\) nên \(\widehat{xOm}=\widehat{mOy}=\frac{\widehat{xOy}}{2}=\frac{40^0}{2}=20^0\)
Vì On là tia phân giác của \(\widehat{yOz}\) nên \(\widehat{yOn}=\widehat{nOz}=\frac{\widehat{yOz}}{2}=\frac{70^0}{2}=35^0\)
Vì Oy nằm giữa Ox và Oz mà Om nằm giữa Oy và Ox, On nằm giữa hai tia Oy và Oz nên Oy nằm giữa Om và Om.
\(\Rightarrow\widehat{mOy}+\widehat{yOn}=\widehat{mOn}\)
hay \(20^0+35^0=\widehat{mOn}\)
\(\Leftrightarrow\widehat{mOn}=55^0\)
Vậy \(\widehat{mOn}=55^0\)