cho tam giác ABC, O nằm trong tam giác. CMR \(\frac{AB+BC+AC}{2}< OA+OB+OC< AB+AC+BC\)

Những câu hỏi liên quan
Cho tam giác ABC biết AB=BC=AC. Giả sử O nằm trong tam giác đó sao cho OA=OB=OC. CMR o là giao điểm của ti
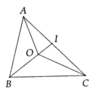
Cho tam giác ABC, điểm O nằm trong tam giác, tia BO cắt cạnh AC tại I. a) So sánh OA và IA + IO, từ đó suy ra OA + OB < IA + IB; b) Chứng minh: OA + OB < CA + CB; c) Chứng minh: (AB+AC+BC) /2 < OA + OB + OC < AB + BC + CA
tam giác ABC,O nằm trong tam giác, OA cắt BC tại M, OB cắt AC tại N, OC cắt AB tại P.CMR (AM/OA)+(BN/OB)+(CP/OC) >=9/2
tam giác ABC,O nằm trong tam giác, OA cắt BC tại M, OB cắt AC tại N, OC cắt AB tại P.CMR (AM/OA)+(BN/OB)+(CP/OC) >=9/2
Cho O là 1 điểm nằm trong tam giác đều ABC,qua O kẻ OI//AB(I thuộc AC),OK//AC(K thuộc BC),OJ//BC(J thuộc AB)
Chứng minh chu vi tam giác IJK=OA+OB+OC
Cho tam giác ABC điểm O nằm trong tam giác, tia BO cắt cạnh AC tại Ia) So sánh OA và IA + IO, từ đó suy ra OA + OB IA + IB;b) Chứng minh OA + OB CA + CB.c) Chứng minh
A
B
+
B
C
+
C
A
2
O
A
+
O
B
+
O...
Đọc tiếp
Cho tam giác ABC điểm O nằm trong tam giác, tia BO cắt cạnh AC tại I
a) So sánh OA và IA + IO, từ đó suy ra OA + OB < IA + IB;
b) Chứng minh OA + OB < CA + CB.
c) Chứng minh A B + B C + C A 2 < O A + O B + O C < A B + B C + C A
Cho tam giác nhọn ABC, BC>AC>BA.O là một điểm nằm bên trong tam giác. OA,OB,OC kéo dài cắt BC,CA,AB lần lượt ở P,Q,R. CMR OP+OR+OQ<BC
Cho tam giác ABC. O là một điểm nắm trong tam giác. CM (AB+AC+ BC)/2 < OA + OB + OC<AB + AC + CB
Ta có: AB < OA + OB (bất đẳng thức tam giác)
AC < OA + OC (bất đẳng thức tam giác)
BC < OB + OC (bất đẳng thức tam giác)
=> AB + AC + BC < 2 (OA + OB + OC) => \(\frac{AB+AC+BC}{2}< OA+OB+OC\)(1)
và OA + OB < BC + AC (kết quả của bài 17 SGK)
OB + OC < AB + AC (kết quả của bài 17 SGK)
OA + OC < AB + BC (kết quả của bài 17 SGK)
=> 2 (OA + OB + OC) < 2 (AB + AC + BC) => OA + OB + OC < AB + AC + BC (2)
Từ (1) và (2) => \(\frac{AB+AC+BC}{2}< OA+OB+OC< AB+AC+BC\)(đpcm)
Đúng 0
Bình luận (0)
cho điểm O nằm trong tam giác ABC.Gọi F,E,P lần lượt là hình chiếu của điểm O trên các cạn AB,BC,CA của tam giác ABC
chứng minh
AB+BC+CA/2<OC+OA+OB<AB+AC+BC









 tham khảo nha
tham khảo nha


