Đáp án cần chọn là: C

Đáp án cần chọn là: D

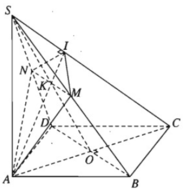
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).

b) Ta có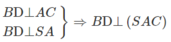 

⇒ BD ⊥ SC

Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).

Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)

Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).

Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).

Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.

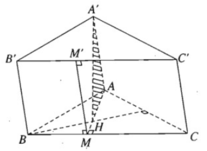
a) BC ⊥ AH và BC ⊥ A'H vì A'H ⊥ (ABC)

⇒ BC ⊥ (A'HA) ⇒ BC ⊥ AA'

Và B'C' ⊥ AA' vì BC // B'C'

b) Ta có AA' // BB' // CC' mà BC ⊥ AA' nên tứ giác BCC’B’ là hình chữ nhật. Vì AA' // (BCC'B') nên ta suy ra MM' ⊥ BC và MM' ⊥ B'C' hay MM’ là đường cao của hình chữ nhật BCC’B’.

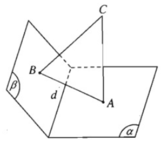
Hai mặt phẳng (α) và (β) không thể trùng nhau vì nếu chúng trùng nhau thì từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với một mặt phẳng, điều đó là vô lí.

Mặt khác (α) và (β) cũng không song song với nhau.

Vì nếu (α) // (β), thì từ CB ⊥ (β) ta suy ra CB ⊥ (α)

Như vậy từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với (α), điều đó là vô lí.

Vậy (α) và (β) là hai mặt phẳng không trùng nhau, không song song với nhau và chúng phải cắt nhau theo giao tuyến d, nghĩa là d = (α) ∩ (β)

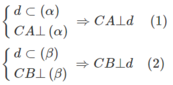
Từ (1) và (2) suy ra d ⊥ (ABC).

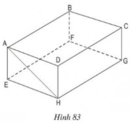
a) BC // FG ⇒ BC // (EFGH)

CD // HG ⇒ CD // (EFGH)

AD // EH ⇒ AD // (EFGH)

Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD

b) CD // AB ⇒ CD // (ABFE)

và CD // (EFGH) ( theo ý a).

c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành

⇒ AH // BG

⇒ AH // (BCGF)

Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).