Cho hình hộp chữ nhật ABCD. A'B'C'D'A'B'C'D'
a) Cm: BD// B'D'
b) Cm: AC// mp(A'B'C'D')
c) Cm: BD//mp(CB'D')
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Gọi M, N lần luợt là trung điểm BD và B'D'
a) Nêu vị trí tương đối của các cặp đường thẳng MN và BD; MNvà CC'; AC và A'D'.
b) Chứng minh MN ^ (A'B'C'D').
c) Biết AA' = 20 cm,AB = 30 cm,AD = 40 cm. Tính B'D'; B'M.
d) Tính thể tích hình hộp
a) Ta có MN cắt BD tại M.
MN//CC', AC và A'D' chéo nhau.
b) MN ^ A'C' và B'D'
c) B'S' = 50cm, B'M = 5 41 c m
d) V =24000cm3
cho hình hộp chữ nhật ABCD. A'B'C'D' . Cm mp( BDA') // mp ( CB'D')
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
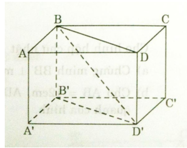
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
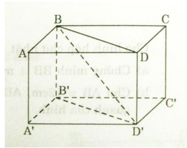
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)
cho hình hộp chữ nhật ABCD A'B'C'D' co AB = 10cm BC = 20 cm AA' = 15 cm
a. tính thể tích hình hộp chữ nhật
b. tính độ dài đường chéo AC'
a) Diện tích đáy hình hộp chữ nhật:
\(AB.AC=10.20=200\left(cm^2\right)\)
Thể tích hình hộp chữ nhật:
\(V=S.h=200.15=3000\left(cm^3\right)\)
b) tam giác A'B'C' vuông tại B. Áp dụng định lý PITAGO ta có:
\(A'C'=\sqrt{A'B'^2+B'C'^2}=\sqrt{10^2+20^2}=10\sqrt{5}\left(cm\right)\)
\(\Rightarrow AC'=\sqrt{AA'+A'C'^2}=\sqrt{15^2+10^2.5}=5\sqrt{29}\left(cm\right)\)
Cho hình bình hành ABCD, trên các cạnh AB, BC, CD, DA theo thứ tự lấy các điển M,N,P,Q sao cho AM=CP,BN=DQ.
a) CM:AMCP là hbh
b)Gọi O là giao điểm 2 đg chéo AC và BD, CM o là trung điểm MP
c)CM:MNPQ là hbh
d)CM: AC,BD,MP,NQ đồng quy tại 1 điểm
a) Vẽ hình chữ nhật ABCD có chiều dài 4 cm, chiều rộng 3 cm. Sau đó nối đỉnh A với đỉnh C, đỉnh B, đỉnh D.
b) Đo chiều dài đoạn thẳng
AC, BD rồi viết số thích hợp vào chỗ chấm:
- AC = …….. cm
- BD = …….. cm
c) Nhận xét:
Độ dài AC …… độ dài BD
(AC, BD là hai đường chéo của hình chữ nhật)
a) Vẽ hình chữ nhật ABCD có chiều dài 4 cm, chiều rộng 3 cm. Sau đó nối đỉnh A với đỉnh C, đỉnh B, đỉnh D.
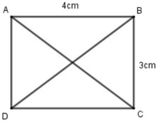
b) Đo chiều dài đoạn thẳng
AC, BD rồi viết số thích hợp vào chỗ chấm:
- AC = 5 cm
- BD = 5 cm
c) Nhận xét:
Độ dài AC = độ dài BD
(AC, BD là hai đường chéo của hình chữ nhật)
Cho hình hộp chữ nhật ABCD A'B'C'D'
a chứng minh rằng ABC'D' là hình chữ nhật
b tính thể tích hình hộp chữ nhật ABCD. A'B'C'D' biết ABCD là hình vuông có cạnh 3 cm và diện tích ABC'D' bằng 18 cm2