Gọi chiều cao của tam giác là h, cạnh đáy tam giác là a. (h, a ∈ ℕ * , a > 3, dm)

Diện tích tam giác ban đầu là 1 2 ah ( d m 2 )

Vì chiều cao bằng 3 4 cạnh đáy nên ta có phương trình:  h = 3 4 a

Nếu chiều cao tăng thêm 3 dm và cạnh đáy giảm đi 3 dm thì diện tích của nó tăng thêm 12  ( d m 2 ) .

Nên ta có phương trình  1 2 h + 3 a − 3 − 1 2 a h = 12

Ta có hệ phương trình:

h = 3 4 a 1 2 h + 3 a − 3 − 1 2 a h = 12 ⇔ h = 3 4 a − 3 h 2 + 3 a 2 = 33 2 ⇔ a = 44 h = 33

(thỏa mãn)

Vậy chiều cao của tam giác bằng 44 dm, cạnh đáy tam giác bằng 33 dm

Suy ra diện tích tam giác ban đầu là 1 2 .44.33 = 726   d m 2

Đáp án: D

Gọi độ dài cạnh đáy là x (dm), x > 2

Suy ra, chiều cao tam giác là

3 4 x (dm)

Vậy diện tích tam giác là:

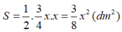
Chiều cao của tam giác khi tăng thêm 3dm là:

3 4 x + 3 (dm)

Cạnh đáy của tam giác khi giảm đi 2dm là: x – 2 (dm)

Vậy diện tích mới của tam giác là:

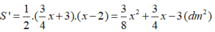
Theo đề bài ta có phương trình:

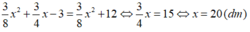
Vậy độ dài cạnh đáy là 20 dm, chiều cao là  3 4 .20 = 15 dm

Gọi cạnh đáy của tam giác ban đầu là \(x\left(dm,x>0\right)\)

Vì tam giác ban đầu có chiều cao bằng \(\frac{3}{4}\)cạnh đáy nên chiều cao của tam giác ban đầu là \(\frac{3}{4}x\)

Diện tích của tam giác ban đầu là \(\frac{1}{2}.x.\frac{3}{4}x=\frac{3}{8}x^2\left(dm^2\right)\)

Vì chiều cao tăng thêm 3dm nên chiều cao của tam giác lúc sau là \(\frac{3}{4}x+3\left(dm\right)\)

Cạnh đáy giảm 2dm nên cạnh đáy của tam giác lúc sau là \(x-2\left(dm\right)\)

Diện tích của tam giác lúc sau là \(\frac{1}{2}\left(\frac{3}{4}x+3\right)\left(x-2\right)\left(dm^2\right)\)

Vì diện tích của tam giác lúc sau lớn hơn diện tích tam giác ban đầu là \(12dm^2\)nên ta có phương trình:

\(\frac{1}{2}\left(\frac{3}{4}x+3\right)\left(x-2\right)-\frac{3}{8}x^2=12\)\(\Leftrightarrow\left(\frac{3}{8}x+\frac{3}{2}\right)\left(x-2\right)-\frac{3}{8}x^2=12\)\(\Leftrightarrow\frac{3}{8}x^2-\frac{3}{4}x+\frac{3}{2}x-3-\frac{3}{8}x^2=12\)\(\Leftrightarrow\frac{3}{4}x=15\Leftrightarrow x=20\)(nhận)

Vậy chiều cao của tam giác ban đầu là 15dm, cạnh đáy ban đầu là 20dm. 

                             Bài làm :

Gọi chiều dài một cạnh cần tính là a (m) ; chiều cao tương ứng là h (m) . Điều kiện : a,h > 0

Thửa ruộng có S=2180 m² 

\(\Rightarrow\frac{a.h}{2}=2180\Rightarrow a.h=4360\Rightarrow a=\frac{4360}{h}\left(1\right)\)

Tăng cạnh 4m ; giảm chiều cao tương ứng 1m thì S không đổi 

\(\Rightarrow\left(a+4\right)\left(h-1\right)=4360\left(2\right)\)

Thay (1) vào (2) ; ta được :

\(\left(\frac{4360}{h}+4\right)\left(h-1\right)=4360\)

\(\Leftrightarrow\frac{\left(4360+4h\right)\left(h-1\right)}{h}=\frac{4360h}{h}\)

\(\Leftrightarrow4h^2+4356h-4360-4360h=0\)

\(\Leftrightarrow4h^2-4h-4360=0\)

\(\Delta'=2^2-4.\left(-4360\right)=17444>0\)

\(\Rightarrow\hept{\begin{cases}h_1=\frac{2+\sqrt{17444}}{4}=\frac{1+7\sqrt{89}}{2}\left(TM\right)\\h_2=\frac{2-\sqrt{17444}}{4}=\frac{1-7\sqrt{89}}{2}\left(KTM\right)\end{cases}}\)

Vậy chiều dài một cạnh cần tính là :

\(\frac{4360}{h}=\frac{4360}{\frac{1+7\sqrt{89}}{2}}=-2+14\sqrt{89}\left(m\right)\)

Ơ quản lí đùa em à đề bài ghi 2180 m² mà lời giải là 180 m² @@ mất gần nửa tiếng số xấu :((

Độ dài cạnh caanjf tìm là 36m

1.Ta thấy\(1\frac{1}{3}:2^3.3=\frac{1}{2}\)nên ta có cách làm như sau :

- Gấp đôi sợi dây 3 lần 

- Trải sợi dây ra và cắt lấy 3 phần dựa theo các dấu gấp.

2.Học kì I,số học sinh giỏi lớp 6A chiếm :\(\frac{3}{3+7}=\frac{3}{10}\)(số học sinh cả lớp)

Cuối năm,số học sinh giỏi lớp 6A chiếm :\(\frac{2}{2+3}=\frac{2}{5}\)(số học sinh cả lớp)

4 học sinh chiếm :\(\frac{2}{5}-\frac{3}{10}=\frac{1}{10}\)(số học sinh cả lớp)

Lớp 6A có :\(4:\frac{1}{10}\)= 40 (học sinh)

3.a) Cạnh hình vuông sau khi tăng 20% thì bằng : 100% + 20% = 120% =\(\frac{6}{5}\)(cạnh ban đầu)

Lúc đó diện tích hình vuông bằng :\(\left(\frac{6}{5}\right)^2=\frac{36}{25}\)= 144% (diện tích ban đầu)

Diện tích hình vuông đã tăng : 144% - 100% = 44%

b) Cạnh hình lập phương sau khi tăng 50% thì bằng : 100% + 50% = 150% =\(\frac{3}{2}\)(cạnh ban đầu)

Lúc đó thể tích hình lập phương bằng :\(\left(\frac{3}{2}\right)^3=\frac{27}{8}\)= 337,5% (thể tích ban đầu)

Thể tích hình lập phương đã tăng : 337,5% - 100% = 237,5%

c) Đáy hình tam giác sau khi tăng 20% thì bằng : 100% + 20% = 120% =\(\frac{6}{5}\)(cạnh đáy ban đầu)

Chiều cao hình tam giác sau khi giảm 20% thì bằng : 100% - 20% = 80% =\(\frac{4}{5}\)(chiều cao ban đầu)

Lúc đó diện tích tam giác bằng :\(\frac{6}{5}.\frac{4}{5}=\frac{24}{25}\)= 96% (diện tích ban đầu)

Diện tích tam giác đã giảm : 100% - 96% = 4%

d) x đồng bằng : 100% - 10% = 90% (giá vốn)

y đồng bằng : 100% + 10% = 110% (giá vốn)

\(\Rightarrow\frac{y}{x}=\frac{11}{9}\)