Dễ dàng thấy ngay rằng các đoạn QM, PN, QP, MN là đường trung bình của các tam giác ADB, CDB, ADC, ABC.

Vậy thì QM song song và bằng PN hay tứ giác MNPQ là hình bình hành.

+) Để hình bình hành MNPQ là hình bình chữ nhật thì \(QM\perp MN\Leftrightarrow AC\perp BD\Leftrightarrow\) Hình bình hành ABCD là hình thoi.

+) Để hình bình hành MNPQ là hình bình thoi thì QM = MN hay AC = BD \(\Leftrightarrow\) Hình bình hành ABCD là hình chữ nhật.

+) Để hình bình hành MNPQ là hình vuông thì nó phải là hình chữ nhật và hình thoi, hay hình bình hành ABCD cũng là hình chữ nhật và hình thoi. Nói cách khác, ABCD phải là hình vuông.

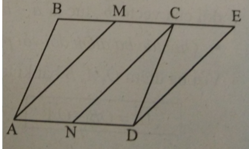
Do ABCD  là hình bình hành nên:  AD = BC.

Lại có; M  và  N lần lượt là  trung điểm của BC; AD  nên :  AN = ND= BM = MC.

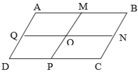
a) Hình trên có tất cả 9 hình bình hành

b) Chu vi hình bình hành ABCD bằng: (4 + 6) x 2 = 20cm

Chu vi hình bình hành AMOQ, BMON, DPOQ và NOPC là: 20 : 4 = 5cm

Chu vi hình bình hành ABNQ, QNDC, AMDP và BMPC là: 20 : 2 = 10cm

Tổng chu vi là: 20 + 5 x 4 + 10 x 4 = 80cm

a.

Do M là trung điểm SA, O là trung điểm AC

\(\Rightarrow OM\) là đường trung bình tam giác SAC \(\Rightarrow OM||SC\Rightarrow OM||\left(SBC\right)\) (1)

N là trung điểm CD, O là trung điểm AC \(\Rightarrow ON\) là đường trung bình ACD

\(\Rightarrow ON||AD\Rightarrow ON||BC\Rightarrow ON||\left(SBC\right)\) (2)

Mà \(ON\cap OM=O\)  ; \(OM;ON\in\left(OMN\right)\) (3)

(1);(2);(3) \(\Rightarrow\left(OMN\right)||\left(SBC\right)\)

b.

J cách đều AB, CD \(\Rightarrow J\) thuộc đường thẳng d qua O và song song AB, CD

- Nếu J trùng O \(\Rightarrow OI\) là đường trung bình tam giác SBD \(\Rightarrow OI||SB\Rightarrow OI||\left(SAB\right)\)

Hay \(IJ||\left(SAB\right)\)

- Nếu J không trùng O, ta có \(\left\{{}\begin{matrix}IO||SB\left(đtb\right)\Rightarrow IO||\left(SAB\right)\\d||AB\Rightarrow IJ||AB\Rightarrow OJ||\left(SAB\right)\end{matrix}\right.\)

\(\Rightarrow\left(OIJ\right)||\left(SAB\right)\Rightarrow IJ||\left(SAB\right)\)

a.

Do M là trung điểm SA, O là trung điểm AC

$\Rightarrow OM$ là đường trung bình tam giác SAC $\Rightarrow OM||SC\Rightarrow OM||\left(SBC\right)$ (1)

N là trung điểm CD, O là trung điểm AC $\Rightarrow ON$ là đường trung bình ACD

$\Rightarrow ON||AD\Rightarrow ON||BC\Rightarrow ON||\left(SBC\right)$ (2)

Mà $ON\cap OM=O$  ; $OM;ON\in \left(OMN\right)$ (3)

(1);(2);(3) $\Rightarrow \left(OMN\right)||\left(SBC\right)$

b.

J cách đều AB, CD $\Rightarrow J$ thuộc đường thẳng d qua O và song song AB, CD

- Nếu J trùng O $\Rightarrow OI$ là đường trung bình tam giác SBD $\Rightarrow OI||SB\Rightarrow OI||\left(SAB\right)$

Hay $IJ||\left(SAB\right)$

- Nếu J không trùng O, ta có {��∣∣��(đ��)⇒��∣∣(���)�∣∣��⇒��∣∣��⇒��∣∣(���){IO∣∣SB(đtb)⇒IO∣∣(SAB)d∣∣AB⇒IJ∣∣AB⇒OJ∣∣(SAB)​

$\Rightarrow \left(OIJ\right)||\left(SAB\right)\Rightarrow IJ||\left(SAB\right)$

ABCD là hbh => NCMA cũng là hình bình hành 

Áp dụng quy tắc hình bình hành => ↓NC + ↓MC = ↓CA ( cái này đễ cho dễ hiểu thì trước tiên gọi O là trung điểm của MN => quy tắc hình bình hành ↓NC + ↓MC = 2↓CO = ↓CA) 

↓AD + ↓NC = ↓AN + ↓ND + ↓NC = ↓AC + ↓ND = ↓AC + ↓MC = 2↓CI ( với I là trung điểm của AM)
↓AM + ↓CD = ↓AB + ↓BM + ↓CD = ↓BM