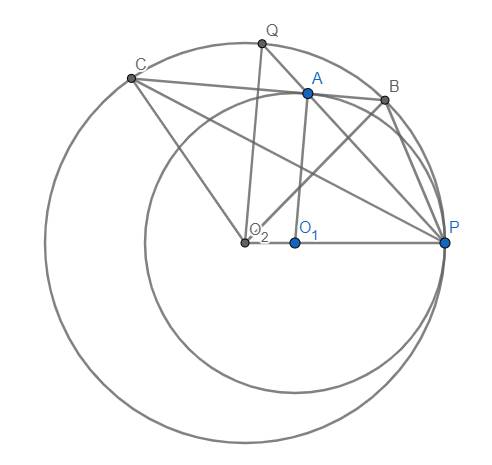
Cho hai đường tròn \(\left(O_1;R_1\right)\) và \(\left(O_2;R_2\right)\) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC (B∈(O\(_1\)) và C ∈ (O\(_2\))). Tiếp tuyến chung tại A của hai đường tròn cắt BC tại I.
a, Chứng minh ΔABC và ΔIO\(_1\)O\(_2\) là các tam giác vuông và BC=2\(\sqrt{R_1R_2}\)
b, Một đường tròn tâm O bán kính R tiếp xúc với đoạn thẳng C và tiếp xúc ngoài với các đường tròn (\(O_1\)), (O\(_2\)). Chứng minh rằng \(\dfrac{1}{\sqrt{R}}=\dfrac{1}{\sqrt{R_1}}+\dfrac{1}{\sqrt{R_2}}\)
c, Giả sử đường tròn (O;R) cố định, còn các đường tròn (\(O_1;R_1\)) và (\(O_2;R_2\)) thay đổi. Tìm giá trị nhỏ nhất của \(R_1.R_2\) theo độ dài R cho trước