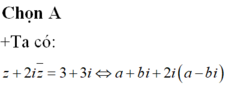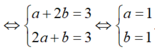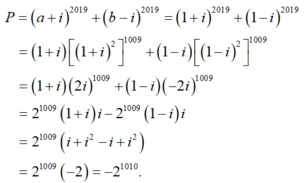cho a - b =7. tính giá trị biểu thức: P = a^2 - ab - 7a + 2019

Những câu hỏi liên quan
Cho các số nguyên dương a; b thỏa mãn 7a^2-1 chia hết cho 7ab-1. Tính giá trị của biểu thức M= a^2019 - b^2019
Câu 1:
a, cho a,b là 2 số thực thỏa mãn điều kiện : a^2+b^2=2(8+ab) và a<b. Tính giá trị của biểu thức P=a^2(a+1)-b^2(b-1)+ab-3ab(a-b+1)+64
b, cho x,y thỏa mãn 2x^2+y^2+9=6x+2xy. Tính giá trị của biểu thức A=x^2019*y^2020-x^2020*y^2019+1/9xy
\(2x^2+y^2+9=6x+2xy\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2-6x+9\right)=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-3\right)^2=0\Leftrightarrow\hept{\begin{cases}x-3=0\\x-y=0\end{cases}}\Leftrightarrow x=y=3\)
\(\Rightarrow A=x^{2019}.y^{2020}-x^{2020}.y^{2019}+\frac{1}{9xy}=\frac{1}{27}\)
Cho các số thực a,b,c thỏa mãn \(a^2+b^2+c^2=3\) và \(a+b+c+ab+bc+ca=6\)
Tính giá trị biểu thức : A=\(\dfrac{a^{30}+b^4+c^{1975}}{a^{30}+b^4+c^{2019}}\)
Tính giá trị biểu thức
1)A=1-3+5-7+.....+2019-2021+2023
2)B=1-2-3+4+5-6-7+8+....+1993-1994
2) \(B=\left(1-2-3+4\right)+\left(5-6-7+8\right)+...+\left(1989-1990-1991+1992\right)+1993-1994\)
\(=0+0+...+0+1993-1994=0+1993-1994=-1\)
\(\frac{a}{2019}\)Cho 3 số a,b,c thỏa mãn a/2019 = b/2020 = c/2021. Tính giá trị biểu thức: M=4*(a-b)*(b-c)-(c-a)^2
gọi a/2019=b/2020=c/2021 là x
\(\Rightarrow\)a=2019*x ;b=2020*x;c=2021*x
\(\Rightarrow\)M=4*(2019*x-2020*x)*(2020-2021)-(2021*x-2019*x)^2
\(\Rightarrow\)M=4*(-x)*(-x)-(2x)^2
\(\Rightarrow\)M=4*x^2-4*x^2
⇒M=0
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức A=(3^2+1)/(3^2-1)+(5^2+1)/(5^2-1)+(7^2+1)/(7^2-1)+...+(2019^2+1)/(2019^2-1)
Cho số phức za+bi,a,b thuộc R thỏa mãn
z
+
2
i
z
¯
3
+
3
i
. Tính giá trị biểu thức:
P
(
a
+
i
)
2019
+
(...
Đọc tiếp
Cho số phức z=a+bi,a,b thuộc R thỏa mãn z + 2 i z ¯ = 3 + 3 i . Tính giá trị biểu thức: P = ( a + i ) 2019 + ( b - i ) 2019
A.![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
cho ba số dương a,b,c thỏa mãn abc=1. CMR A=1/a^2 + 2b^2 +3 + 1/b^2+ 2c^2 +3 + 1/c^2+ 2a^2 +3 <= 1/2
Với 1/a + 1/b + 1/c = 1/(a + b + c) thì không thể nào có ĐK : a = b = c vì nó sẽ như sau :
1/a + 1/b + 1/c = 1/(a + b + c)
=> 3/a = 3/b = 3/c = 1/(a x 3) = 1/(b x 3) = 1/(c x 3) (rất vô lý)
Với 1/(a + b + c) thì phần tử rất nhỏ .
=> Dữ liệu không tồn tại.
Cho a + b + c = 2019 và 1/a+b + 1/a+c + 1/b+c = 1/2019. Tính giá trị của biểu thức S = a/b+c + b/a+c + c/a+b