lấy 9 điểm phan biệt nằm trong hình vuông abcd co cạnh =2 sao cho ko có bất ki 3 điểm nào thẳng hàng .cm tồn tại 3 trong 9 điểm taoh nên 1 tam giác có diện tich bé hơn 1

Những câu hỏi liên quan
Cho \(\Delta ABC\) và 9 điểm nằm trong tam giác đó. Biết trong 9 điểm đã cho không có 3 điểm nào thẳng hàng. Chứng minh rằng tồn tại ít nhất 3 điểm trong 9 điểm đã cho tạo thành 1 tam giác có diện tích nhỏ hơn 1/4 diện tích tam giác ABC
Gọi M,N,P lần lượt là trung điểm các cạnh AB,AC,BC
Do đó diện tích AMN = diện tích BMP = diện tích ANP = \(\frac{1}{4}\) diện tích ABC
Theo nguyên lý di - rich - le thì trong 9 điểm đề bài cho,ít nhất có 3 điểm nằm trong tam giác AMN,BMP hoặc tam giác ANP
Gọi 3 điểm đó là H,I,K
Chẳng hạn 3 điểm H,I,K nằm trong tam giác ANP
= > diện tích HIK < diện tích ANP = \(\frac{1}{4}\) diện tích tam giác ABC
Vậy sẽ có một tam giác nhỏ hơn \(\frac{1}{4}\) diện tích tam giác ABC
Đáp số : Sẽ có một tam giác nhỏ hơn \(\frac{1}{4}\) diện tích tam giác ABC
Đúng 0
Bình luận (0)
Sorry bạn na , mk mới lớp 5 chẳng hiểu gì hết
Đúng 0
Bình luận (0)
hichic...mk cx zậy, ms hc lp 5 thui à!!!:"(((
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Ở trong 1 miền đa giác lồi có 2018 cạnh có diện tích bằng 1 lấy 2017 điểm trong đó ko có 3 điểm nào thẳng hàng CMR: luôn tồn tại một tam giác có đỉnh lấy từ 4035 điểm trên (2018 đinh của đa giác và 2017 điểm đã cho) có diện tích ko quá 1/6050
Bên trong hình vuông có cạnh 5cm cho 51 điểm, trong đó không có 3 diểm nào thẳng hàng. Chứng minh rằng luôn tồn tại một tam giác có 3 đỉnh là 3 điểm đã cho mà có diện tích không lớn hơn 0.5cm2.
chia hình vuông thành 25 hình vuông nhỏ có cạnh bằng 1cm ( nghĩa là diện tích bằng 1cm^2)
Theo nguyên lí dirichlet do có 51 điểm và 25 hình vuông
nên tồn tại một hình vuông con chứa ít nhất 3 điểm
Nên 3 điểm đỏ taoh thành 1 tma giác có diện tích nhỏ hơn 1/2 diện tích hình vuông nhỏ là 0,5 cm^2
Vậy ta có điều phải chứng minh
Cho tứ giác ABCD có diện tích bằng 10 Bên trong tứ giác lấy 4 điểm phân biệt để cùng với 4 đỉnh của tứ giác có 8 điểm trong đó không có 3 điểm nào thẳng hàng. Chứng minh tồn tại ít nhất một tam giác có 3 đỉnh lấy từ 8 điểm nói trên có S không vượt quá 1.
Ở miền trong 1 đa giác lồi 2018 cạnh có diện tích bằng 1 lấy 2017 điểm trong đó ko có 3 điểm nào thẳng hàng CMR: luôn tồn tại 1 tam giác có đỉnh lấy từ 3035 điểm trên (gồm 2018 đinh của đa gicas và 2017 điểm đã cho) có diện tích không vượt quá 1/6050
Cho 15 điểm phân biệt, trong đó có 6 điểm thẳng hàng, trong số 9 điểm còn lại không có 3 điểm nào
thẳng hàng và không có 2 điểm nào thẳng hàng với bất kì 1 điểm nào đó trong 6 điểm nêu ở trên. Hỏi có bao
nhiêu tam giác mà các đỉnh của chúng lấy từ 15 điểm đã cho?
Chọn 3 điểm trong 15 điểm có: \(C^3_{15}\)(cách chọn)
Chọn 3 điểm trong 6 điểm thẳng hàng có:\(C^3_6\)(cách)
=>Số tam giác được tạo thành từ 15 điểm đã cho là: \(C^3_{15}-C^3_6\)(tam giác)
Đúng 1
Bình luận (0)
Cho ΔABC và 9 điểm nằm trong tam giác đó. Biết trong 9 điểm đã cho không có 3 điểm nào thẳng hàng. Chứng minh rằng tồn tại ít nhất 3 điểm trong 9 điểm đã cho tạo thành 1 tam giác có diện tích nhỏ hơn 1/4 diện tích tam giác ABC.giúp mik nha
Đọc tiếp
Cho ΔABC và 9 điểm nằm trong tam giác đó. Biết trong 9 điểm đã cho không có 3 điểm nào thẳng hàng. Chứng minh rằng tồn tại ít nhất 3 điểm trong 9 điểm đã cho tạo thành 1 tam giác có diện tích nhỏ hơn 1/4 diện tích tam giác ABC.giúp mik nha ![]()
Gọi M ,N ,P lần lượt là trung điểm các cạnh AB ,AC , BC . Do đó \(S_{AMN}=S_{BMP}=S_{ANP}=\frac{1}{4}S_{ABC}\)
Theo nguyên lí di-rich-le thì trong chín điểm đề bài cho, có ít nhất ba điểm nằm trong tam giác AMN,BMP,ANP gọi 3 điểm đó là H , I , K
chẳng hạn 3 điểm H,I,K nằm trong ANP
\(\Rightarrow S_{HIK}< S_{ANP}=\frac{1}{4}S_{ABC}\)
Vậy sẽ có một tâm giác nhỏ hơn 1/4 diện tích tam giác ABC
Đúng 0
Bình luận (0)
Cho 65 điểm, không có 3 điểm nào thẳng hàng nằm bên trong một hình vuông có cạnh bằng 1. Chứng minh rằng, luôn tìm được 5 điểm trong 65 điểm đó thỏa mãn: các tam giác được tạo bởi 3 điểm bất kì trong 5 điểm đó có diện tích không quá \(\frac{1}{32}\).
cho n điểm trong mp sao cho ko có 3 điểm nào thẳng hàng và 3 điểm bất kỳ tạo thành 1 tam giác có diện tích \(\le\) 1.CMR n điểm đã cho thuộc 1 tam giác có diện tích \(\le\) 4
Do số tam giác được lập từ n điểm đã cho là hữu hạn nên tồn tại 1 tam giác ABC có diện tích lớn nhất.
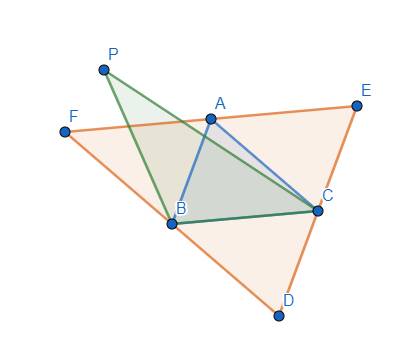
Dựng tam giác DEF sao cho A, B, C lần lượt là trung điểm của EF, DF, DE. Khi đó vì \(S_{ABC}\le1\) nên \(S_{DEF}\le4\). Ta sẽ chứng minh tam giác DEF chính là tam giác cần tìm.
Thật vậy, giả sử tồn tại điểm P trong số n điểm đã cho nằm ngoài tam giác DEF. Không mất tính tổng quát, giả sử P nằm khác phía BC đối với EF. Khi đó khoảng cách từ P đến BC sẽ lớn hơn khoảng cách từ A đến BC, dẫn đến \(S_{PBC}>S_{ABC}\), điều này là vô lí vì ta đã giả sử tam giác ABC là tam giác có diện tích lớn nhất trong số các tam giác tạo thành từ n điểm đã cho \(\Rightarrow\) tam giác DEF thỏa ycbt
Vậy ta có đpcm.
,
Đúng 2
Bình luận (0)
Nếu bạn không xem được phần trả lời của mình thì vào trang cá nhân của mình xem nhé, tại câu trả lời của mình có vẽ hình nên nó không đăng lên được ngay.
Đúng 1
Bình luận (0)



















