Tìm giá trị nhỏ nhât của A = \(|x-2|+5\)
Giải chi tiết ra hộ mình nha !
Những câu hỏi liên quan
Anh em giải chi tiết hộ mình bài toán nỳ được không.
a) Cho 3 số dương a,b,c có a+b+c=1. Chứng minh rằng 1/a+1/b+1/c≥9
b) Tìm giá trị nhỏ nhât của biểu thức A=a⁴-2a³+3a²-4a+5
c) Giải phương trình: x²-3x+2+|x-1|=0
a) \(VT=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)\(=\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\) (vì a+b+c = 1)
\(=3+\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}\)
\(=3+\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)\)
C/m BĐT phụ: \(\frac{x}{y}+\frac{y}{x}\ge2\) với x,y dương
\(\Leftrightarrow\)\(x^2+y^2\ge2xy\)
\(\Leftrightarrow\) \(x^2-2xy+y^2\ge0\)
\(\Leftrightarrow\) \(\left(x-y\right)^2\ge0\) luôn đúng
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=y\)
Áp dụng BĐT trên ta có: \(\frac{a}{b}+\frac{b}{a}\ge2;\) \(\frac{a}{c}+\frac{c}{a}\ge2;\) \(\frac{b}{c}+\frac{c}{b}\ge2\)
\(\Rightarrow\)\(VT=3+\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)\ge3+2+2+2=9\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(a=b=c\)
Vậy \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge9\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(a=b=c\)
Đúng 0
Bình luận (0)
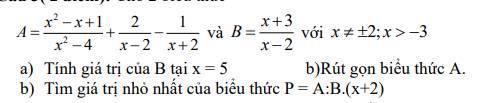
Giải hộ mình chi tiết câu tìm giá trị nhỏ nhất nha.
Lời giải:
a.
Tại $x=5$ thì $B=\frac{5+3}{5-2}=\frac{8}{3}$
b.
\(A=\frac{x^2-x+1}{(x-2)(x+2)}+\frac{2(x+2)}{(x-2)(x+2)}-\frac{x-2}{(x-2)(x+2)}=\frac{x^2-x+1+2(x+2)-(x-2)}{(x-2)(x+2)}\)
\(=\frac{x^2+7}{(x-2)(x+2)}\)
c.
\(P=A:B(x+2)=\frac{x^2+7}{(x-2)(x+2)}:\frac{x+3}{x-2}.(x+2)=\frac{x^2+7}{x+3}\)
Áp dụng BĐT Cô-si:
$x^2+1\geq 2|x|\geq 2x$
$\Rightarrow x^2+7\geq 2x+6=2(x+3)$
$\Rightarrow P\geq \frac{2(x+3)}{x+3}=2$
Vậy $P_{\min}=2$. Giá trị này đạt tại $x^2=1\Leftrightarrow x=\pm 1$ (tm)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của các biểu thức:
a) A= |x-1|+|x-2|+....+|x-10|
b)B=|3x-6|+|y2+1|+2015
Nhớ giải chi tiết hộ mình nha , gấp lắm các bạn ạ!
Ai giải đầy đủ ,chi tiết mà đúng thì mình sẽ k cho
tìm giá trị nhỏ nhất của bt A =x^2-6x+11 giải chi tiết cho mình nha
\(A=x^2-6x+11\)
\(\Leftrightarrow A=x^2-2.3x+9+2\)
\(\Leftrightarrow A=\left(x-3\right)^2+2\ge2\)
\(\Leftrightarrow A_{min}=2\)
\(\Leftrightarrow x-3=0\)
\(x=3\)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất
B = 2x^2 + 3x + 2
Tìm giá trị lớn nhât
C = -2x^2 - 4x + 2
giải chi tiết giùm mình nha
Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất
a, A=|x-2|+|y+5|_10
b, B=-(x-5)^2+9
Giải chi tiết ra cho mình với nhé
Tìm giá trị nhỏ nhất của
M= x^2 - 3x + 5
N= 2 / 8x - 4x^2 - 5
giải chi tiết giùm mình nha mình like cho
a/ \(M=x^2-2.\frac{3}{2}x+\left(\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2+5\)
\(=\left(x-\frac{3}{2}\right)^2+\frac{11}{4}\ge\frac{11}{4}\)
Vậy Min M = 11/4 khi x - 3/2 = 0 => x = 3/2
b/ \(N=-\left(4x^2-\frac{2}{8}x+5\right)\)
\(=-\left[\left(2x\right)^2-2.2x.\frac{1}{16}+\left(\frac{1}{16}\right)^2-\left(\frac{1}{16}\right)^2+5\right]\)
\(=-\left(2x-\frac{1}{16}\right)^2-\frac{1279}{256}\ge-\frac{1279}{256}\)
Vậy Min N = -1279/256 khi 2x - 1/16 = 0 => 2x = 1/16 => x = 1/32
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất :
B= x-x^2
N = 2x - 2x^2 - 5
Tìm giá trị nhỏ nhất :
M = x^2 + y^2 - x + 6y + 10
Làm ơn giải chi tiết hộ mình vs
Thanks nhìu
Tìm giá trị nhỏ nhất của biểu thức: A = | x - 1 | + | x - 2018 |
GIẢI CHI TIẾT GIÙM MÌNH NHA! CẢM ƠN
Ta có \(\left|x+1\right|\ge0\)với mọi giá trị của x
và \(\left|x-2018\right|\ge0\)với mọi giá trị của x
=> \(\left|x+1\right|+\left|x-2018\right|\ge0\)với mọi giá trị của x
Vậy GTNN của A là 0.
Đúng 0
Bình luận (0)
