Hãy chứng tỏ Ax // BC ; AB // Cz ; By // AC.
 Mong mọi người giúp đỡ mình ! Mình cảm ơn !
Mong mọi người giúp đỡ mình ! Mình cảm ơn !
cho tam giác ABC có B=C=40 độ. Gọi Ax là tia phân giác của góc ở ngoài đỉnh A. Hãy chứng tỏ Ax// BC
Cho tam giác ABC có góc B = C = 40 độ.Gọi Ax là tia phân giác của góc ngoài ở đỉnh A . Hãy chứng tỏ rằng Ax // BC.
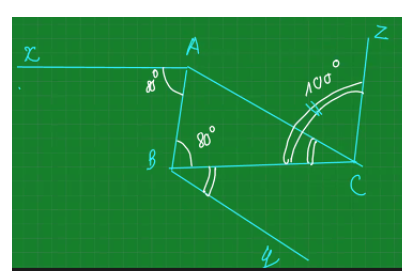
\(\widehat{BAC}=180^o-\left(\widehat{B}+\widehat{C}\right)=180^o-80^o=100^o\)
\(\widehat{yAc}=180^o-100^o=80^o\)
Mà tia Ax là tia phân giạc góc ngoài của A
\(\Rightarrow\widehat{yAx}=\widehat{xAC}=\frac{\widehat{yAc}}{2}=\frac{80^o}{2}=40^o\)
Ở vị trí so le trong => Ax//BC
Cho tam giác ABC có góc B = góc C = 40 độ . Gọi Ax là tia phân giác của góc ngoài ở đỉnh A . Hãy chứng tỏ rằng Ax // BC
Tam giác ABC có: góc B +góc C + góc BAC = 180o => 40o + 40o + BAC = 180o => góc BAC = 180o - 80o = 100o
=> góc BAy = 180o - BAC = 180o - 100o = 80o (do BAy là góc ngoài tam giác )
=> góc xAB = yAB/2 = 80o/2 = 40o (do Ax là p/g của góc yAB)
=> góc xAB = ABC (= 40o) Mà hai góc này ở vị trí SLT => Ax // BC
Cho tam giác ABC có góc B= góc C = 40 độ . Gọi Ax là tia phân giác của góc ngoài ở đỉnh A . Hãy chứng tỏ rằng Ax song song với BC
Cho tam giác ABC, góc B= góc C= 53° Gọi tia Ay là tia đối của tia AB. Vẽ Ax song song với BC. Hãy chứng tỏ rằng Ax là phân giác của góc CAy
Áp dụng tc góc ngoài: \(\widehat{yAC}=\widehat{B}+\widehat{C}=2\widehat{C}\)
Vì Ax//BC nên \(\widehat{xAC}=\widehat{C}\) (so le trong)
Do đó \(2\widehat{xAC}=\widehat{yAC}\)
Vậy Ax là p/g CAy
Cho tam giác ABC có \(\widehat{B}=\widehat{C}=40^0\). Gọi Ax là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng tỏ Ax // BC ?
Giải
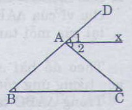
= + (góc ngoài của tam giác ABC)
= 400+ 400 = 800
400.
Hai góc so le trong bằng nhau nên Ax// Bc
Cho tam giác ABC có góc B bằng góc C và có số đo là 40 độ. Gọi Ax là tia phân giác của góc ngoài ở đỉnh. Hãy chứng tỏ rằng Ax song song với BC.
Tam giác ABC có: góc B +góc C + góc BAC = 180 o => 40 o + 40 o + BAC = 180 o => góc BAC = 180 o - 80 o = 100 o
=> góc BAy = 180 o - BAC = 180 o - 100 o = 80 o (do BAy là góc ngoài tam giác )
=> góc xAB = yAB/2 = 80 o/2 = 40 o (do Ax là p/g của góc yAB)
=> góc xAB = ABC (= 40 o) Mà hai góc này ở vị trí SLT => Ax // BC
Cho tam giác ABC có góc B=C=40 độ . Gọi Ax là tia phân giác của góc ngoài ở đỉnh A . Hãy chứng tỏ Ax song song với BC .
Giải giúp cho mình với đi !! Mình sẽ tick cho mấy bạn !!
Ta có góc B=góc C=40 độ=> góc A= 180 độ- góc B- góc C= 100 độ => góc ngoài của góc A là 80 độ
Ax là phân giác của góc ngoài ở đỉnh A=> góc tạo bởi Ax và AB là 40 độ mà góc B=40 độ=> góc đó=góc B mà 2 góc ở vị trí so le trong=> Ax//BC
Các thầy( cô ) và các bạn giúp em với nhé ( giải thích cho em cách làm ) : Cho tam giác ABC có B=C=40độ . Gọi Ax là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng tỏ rằng Ax // BC.
(bạn tự vẽ hình nha )
Gọi hai góc tạo bởi tia Ax và góc ngoài tại đỉnh A của tg ABC là góc A1 và góc A2
Ta có:góc ngoài tại đỉnh A của tg AB = <B +<C(tính chất góc ngoài của tg) = 40+40 =80
Vì Ax là tia pg của góc ngoài đỉnh A của tgABC nên : <A1=<A2 =1/2*80 =40
Ta có : <A 1=<B (hoăc C / tùy theo cách vẽ ) căp góc ở vị trí SLT
=> Ax // BC