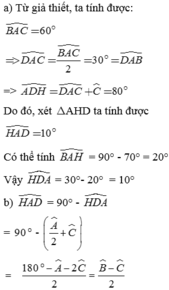Cho tam giác abc ,biết b>c kẻ đường cao ah và tia phân giác ad. Cmr: had= (b-c) :2

Những câu hỏi liên quan
Cho tam giác ABC có
B
^
C
^
. Từ đỉnh A kẻ đường cao AH và tia phân giác AD.a) Biết
B
^
70
°
,
C
^
50
°
, tính số đo
H
A
D
^
.b) Chứng minh
H...
Đọc tiếp
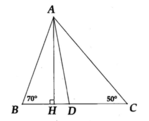
Cho tam giác ABC có B ^ > C ^ . Từ đỉnh A kẻ đường cao AH và tia phân giác AD.
a) Biết B ^ = 70 ° , C ^ = 50 ° , tính số đo H A D ^ .
b) Chứng minh H A D ^ = B ^ − C ^ 2
cho tam gics ABC biết góc B> góc C . kẻ đường cao AH và phân giác AD,
a) CMR :GÓC HAD = GÓC B - GÓC C / 2
Cho tam giác ABC vuông ở A, có B > C. Kẻ đường cao AH, đường trung tuyến AM và đường phân giác AD. Giả sử AH, AM chia BAC thành ba góc bằng nhau
a, Chứng minh AD cũng là tia phân giác của HDM
b, B = CAH
c, Tính B, C và HAD
cho tam giác ABC có góc B>C. kẻ đường cao AH và đường phân giác AD. CMR: AD nằm giữa AH và AC
cho tam giác ABC góc B > góc C kẻ đường cao AH và đường phân giác AD
a, chứng minh Góc HAD = ( B - C ) /2
b,Tính góc A biết góc HAD =15 độ và 3B=5C
Cho tam giác ABC, đỉnh B là góc tù.Có AD là tia phân giác và có AH là đường cao. CMR
a)2.HAD=HAB+CAD
b)ABC=90*+HAB
Bài 1: Cho tam giác ABC có AB AC. kẻ AE là tia phân giác của góc BAC ( E thuộc BC). CMR:a) Tam giác ABE tam giác ACEb) AE là đường trung trực của đoạn thằng BC.Bài 2: Cho tam giác ABC, đường cao AH. Trên nửa mặt phảng bờ AC không chứa B, vẽ tam giác ACD sao cho AD BC; CD AB. CMR:a) AB song song với CDb) AH vuông góc với AD.Bài 3: Cho tam giác ABC vuông tại A. Biết tam giác ABC tam giác DEF; tam giác DEF tam giác HIK và AB 2cm; DF 2cm. CMR: Tam giác HIK là tam giác vuông cân.Bài 4: Cho t...
Đọc tiếp
Bài 1: Cho tam giác ABC có AB = AC. kẻ AE là tia phân giác của góc BAC ( E thuộc BC). CMR:
a) Tam giác ABE = tam giác ACE
b) AE là đường trung trực của đoạn thằng BC.
Bài 2: Cho tam giác ABC, đường cao AH. Trên nửa mặt phảng bờ AC không chứa B, vẽ tam giác ACD sao cho AD = BC; CD = AB. CMR:
a) AB song song với CD
b) AH vuông góc với AD.
Bài 3: Cho tam giác ABC vuông tại A. Biết tam giác ABC = tam giác DEF; tam giác DEF = tam giác HIK và AB = 2cm; DF = 2cm. CMR: Tam giác HIK là tam giác vuông cân.
Bài 4: Cho tam giác ABC = tam giác DEF. Biết 2 tia phân giác của góc B và góc C cắt nhau tại O tạo thành góc BOC = 135 độ và góc B = 2 lần góc C. Tính các góc của tam giác DEF.
( bạn tự vẽ hình)
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.
Đúng 0
Bình luận (0)
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.
Cho tam giác ABC có góc B>góc C. Đường phân giác AD kẻ AH vuông góc với BC.
CMR góc HAD =góc B-góc C/2
cho tam giác ABC có B>C Kẻ đường cao AH và AD là tia phân giác a)Tính ADC và ADB theo B,C