Giải và biện luận \(|\sqrt{x-4}-1|+\sqrt{x-4}-2|\)

Những câu hỏi liên quan
Giải và biện luận pt \(\sqrt{x-3-2\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}=a\left(x\ge4\right)\)
Giải và biện luận pt :
\(\sqrt{x^3+3x^2+3x+1}+m\sqrt{x^2-4x-4}=2\) (1)
\(\left(1\right)\Leftrightarrow\sqrt[3]{\left(x+1\right)^3}+m\sqrt{\left(x-2\right)^2}=2\)
\(\Leftrightarrow x+1+m\left|x-2\right|=2\) (2)
Xét \(x\ge2\)thì (2) \(\Leftrightarrow x+1+m\left(x-2\right)=2\)
\(\Leftrightarrow\left(m+1\right)x=2m+1\)(3)
Nếu m = -1 thì (3) vô nghiệm
m khác -1 thì (3) có nghiệm x = \(\frac{2m+1}{m+1}\)
Vì \(x\ge2\)nên \(\frac{2m+1}{m+1}\ge2\Leftrightarrow\frac{2m+1}{m+1}-2\ge0\)
\(\Leftrightarrow m< -1\)
Nếu m < -1 thì phương trình có nghiệm \(\frac{2m+1}{m+1}\)
m > -1 phương trình vô nghiệm
m = -1 , \(x=\frac{3}{2}\)
Xét x < 2 thì (2) <=> x + 1 - m(x - 2) = 2
<=> (1-m)x = 1-2m (4)
Nếu m = 1 thì (4) vô nghiệm
m khác 1 (4) có nghiệm \(x=\frac{1-2m}{1-m}\)
Vì \(\frac{1-2m}{1-m}< 2\Leftrightarrow m< 1\)
KL : nếu m < -1 : \(x=\frac{2m+1}{m+1}\)
Đúng 0
Bình luận (0)
(x-2)^2 sai nhé thằng óc lz ????? copyy bài người khac nhưng éo để ý đề à ??? -4 éo phải +4
Đúng 0
Bình luận (0)
thằng number one mà sửa lại -4 thành +4 ý
thì m là súc vật tự đăng tự trả lời ?? copyy đề trên mạng ??? xong vô đây tự đăng tự trả lời sv
Đúng 0
Bình luận (0)
Cho pt: \(\sqrt{x^2-4}=x-a\)
1. Giải PT a=2
2. giải và biện luận theo a
giải và biện luận \(\sqrt{x+a}+\sqrt{x-a}=\sqrt{2a}\)
Lời giải:
TH1: $a< 0$ thì PT không tồn tại
TH2: $a=0$ thì PT có nghiệm duy nhất $x=0$
TH3: $a>0$
PT $\Leftrightarrow 2x+2\sqrt{(x-a)(x+a)}=2a$
$\Leftrightarrow (x-a)+\sqrt{(x-a)(x+a)}=0$
$\Leftrightarrow \sqrt{x-a}(\sqrt{x-a}+\sqrt{x-a})=0$
$\Leftrightarrow \sqrt{x-a}.\sqrt{2a}=0$
$\Leftrightarrow \sqrt{x-a}=0$
$\Leftrightarrow x=a$.
Kết luận:
$a<0$ thì PT không tồn tại
$a\geq 0$ thì pt có nghiệm duy nhất $x=a$
Đúng 1
Bình luận (0)
giải và biện luận phương trình:
\(\left(x-m\right)\sqrt{x-1}=x^2-m^2\)
a, Vẽ đồ thị hàm số y= \(\sqrt{4x^2-4x+1}\) + \(\sqrt{x^{2^{ }}-4x+4}\)
b, Biện luận theo m số nghiệm của phương trình:
\(\sqrt{4x^{2^{ }}-4x+1}\)+ \(\sqrt{x^{2^{ }}-4x+4}\) = m
\(y=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(x-2\right)^2}=\left|2x-1\right|+\left|x-2\right|\)
\(y=\left[{}\begin{matrix}3x-3\left(\text{với }x\ge2\right)\\3-3x\left(\text{với }x\le\dfrac{1}{2}\right)\\x+1\left(\text{với }\dfrac{1}{2}\le x\le2\right)\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau:
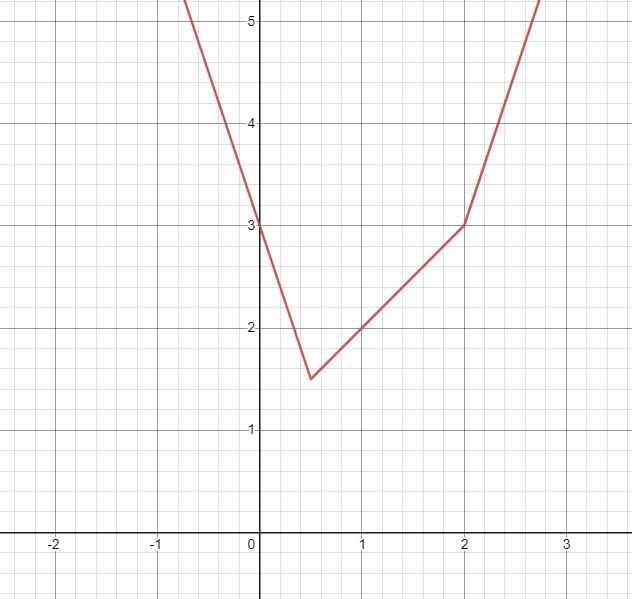
Từ đồ thị ta thấy phương trình \(\sqrt{4x^2-4x+1}+\sqrt{x^2-4x+4}=m\):
- Có đúng 1 nghiệm khi \(m=\dfrac{3}{2}\)
- Có 2 nghiệm phân biệt khi \(m>\dfrac{3}{2}\)
- Vô nghiệm khi \(m< \dfrac{3}{2}\)
Đúng 0
Bình luận (0)
\(A=\left(\frac{2+\sqrt{x}}{2-\sqrt{x}}-\frac{2-\sqrt{x}}{2+\sqrt{x}}+\frac{4x}{4-x}\right):\frac{\sqrt{x}-3}{2\sqrt{x}-x}\)
a) rút gọn A
b) tìm các giá trị của x để A > 0
c) giải và biện luận phương trình: mx + 1 = \(m^2\)+ x với m là tham số
a:dk: x>0;x khac 1; x khac 2
A=mở ngoăc vuông (2+căn x)^2-(2-căn x)^2+4x tất ca trên (4-x) đống ngăc vuông nhân voi (2căn x -x)/(căn x - x)
rút gon ngoăc vuông ta co (8căn x +4x)/(4-x) roi nhân vơi (2 căn x -x)/(căn x -3) rôi rút gon thu dươc 4x/(căn x -3)
b:4x/(Cx -3) > 0 * vi x >0 nen 4x > 0. vay muôn A>0 thi Cx-3 > 0 tương đương Cx>3 tương đương x>9
c; não quá tải. đợij lần sau
Đúng 0
Bình luận (0)
Giải và biện luận phương trình sau: \(\frac{x}{\sqrt{x+m}}=\frac{x}{\sqrt{x+1}}\)
giải và biện luận pt sau:
1.\(\left(m^2-4m+3\right)x-m^2+3m-2=0\)
2.\(\dfrac{x^2-m}{x-1}+m=x+1\)
3. \(\dfrac{2x+m}{\sqrt{x-1}}-4\sqrt{x-1}=\dfrac{x-2m+3}{\sqrt{x-1}}\)













