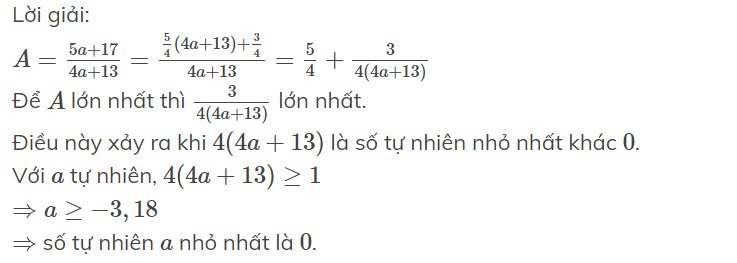Với giá trị nào của số tự nhiên a để phân số \(\frac{6a-13}{5a-17}\) có giá trị lớn nhất

Những câu hỏi liên quan
Với giá trị nào của số tự nhiên a thì phân số \(\frac{6a-13}{5a-17}\)có giá trị lớn nhất
với giá trị nào của số tự nhiên a thì phân số 6a-13/5a-17 có giá trị lớn nhất
Với giá trị nào của số tự nhiên a thì phân số (5a+17)/(4a+13) có giá trị lớn nhất, giá trị đó là bao nhiêu?
Với giá trị nào của số tự nhien a thì phân số \(\frac{6a-13}{5a-17}\)có gái trị lớn nhất
nói cách làm nhé ^_^
Với giá trị nào của số tự nhien a thì phân số \(\frac{6a-13}{5a-17}\)có gái trị lớn nhất
nói cách làm nhé ^_^
Với giá trị nào của số tự nhien a thì phân số \(\frac{6a-13}{5a-17}\) có gái trị lớn nhất
Với giá trị nào của số tự nhiên a thì phân số 6a-13/5a-17
Để \(\frac{6a-13}{5a-17}\inℤ\)
=> \(6a-13⋮5a-17\)
=> 5(6a - 13) \(⋮\)5a - 17
=> 30a - 65 \(⋮\)5a - 17
=> 30a - 102 + 37 \(⋮\)5a - 17
=> 6(5a - 17) + 37 \(⋮\)5a - 17
Vì \(6\left(5a-17\right)⋮5a-17\)
=> 37 \(⋮\)5a - 17
=> 5a - 17 \(\in\)Ư(37)
=> \(5a-17\in\left\{1;-1;37;-37\right\}\)
=> a \(\in\left\{\frac{18}{5};\frac{16}{5};\frac{54}{5};-4\right\}\)
Vì a là số tự nhiên => a \(\in\varnothing\)
Với giá trị nào của số tự nhiên a thì (5a+17)/(4a+13) có giá trị lớn nhất ?
Lời giải:
$\frac{5a+17}{4a+13}=\frac{\frac{5}{4}(4a+13)+\frac{3}{4}}{4a+13}$
$=\frac{5}{4}+\frac{3}{4(4a+13)}$
Để phân số trên max thì $\frac{3}{4(4a+13)}$ max
Điều này xảy ra khi $4a+13$ là số nguyên dương nhỏ nhất.
Với $a$ là stn, $4a+13$ là số nguyên dương nhỏ nhất khi $a$ nhỏ nhất, bằng $0$
Vậy $a=0$
Đúng 0
Bình luận (0)
Với giá trị nào của số tự nhiên a thì biểu thức: P=5a+17/4a+13 có giá trị lớn nhất