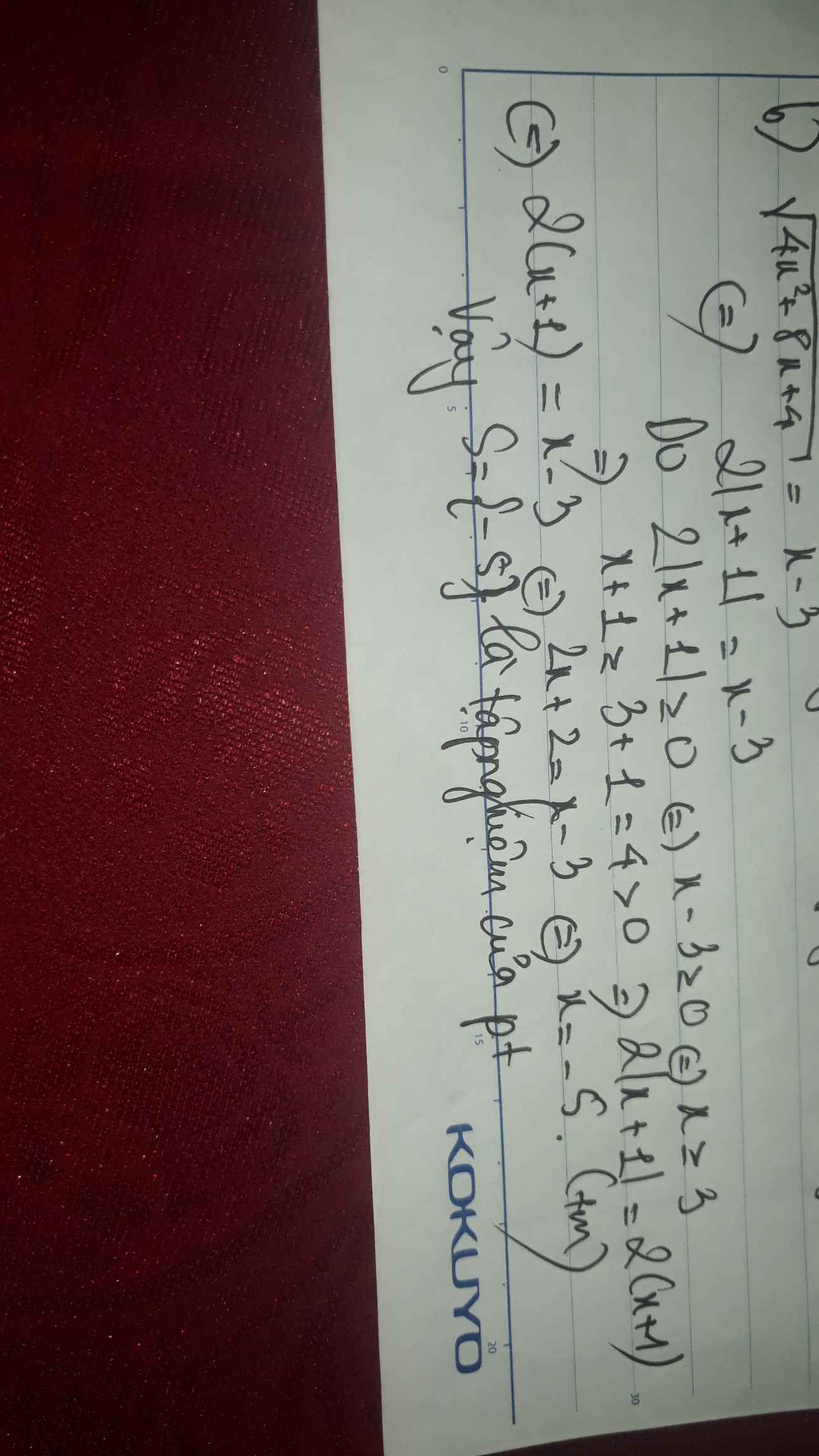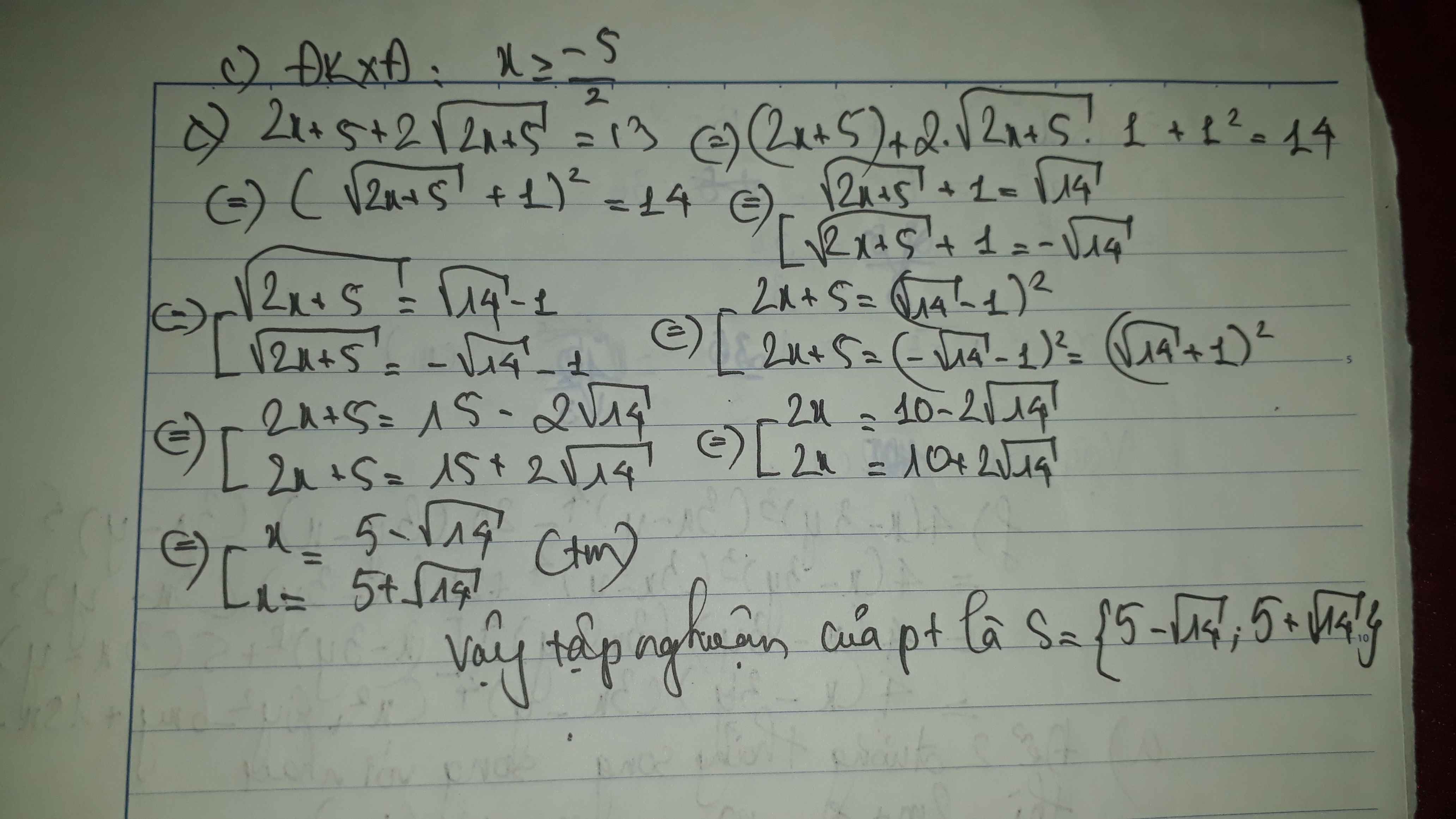ĐKXĐ : \(x>-\frac{3}{2}\)

pt \(\Leftrightarrow2\left(x+1\right)\left(2x+3\right)=8x^2+18x+11\)

\(\Leftrightarrow2x^2+10x+6=8x^2+18x+11\)

\(\Leftrightarrow6x^2+8x+5=0\)

\(\Leftrightarrow6\left(x^2+\frac{4}{3}x+\frac{5}{6}\right)=0\)

\(\Leftrightarrow6\left(x+\frac{2}{3}\right)^2+\frac{7}{3}=0\) ( ***** )

Vậy pt vô nghiệm

a.

\(3\sqrt{-x^2+x+6}\ge2\left(1-2x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-x^2+x+6\ge0\\1-2x< 0\end{matrix}\right.\\\left\{{}\begin{matrix}1-2x\ge0\\9\left(-x^2+x+6\right)\ge4\left(1-2x\right)^2\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-2\le x\le3\\x>\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\25\left(x^2-x-2\right)\le0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}< x\le3\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\-1\le x\le2\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow-1\le x\le3\)

b.

ĐKXĐ: \(x\ge0\)

\(\Leftrightarrow\sqrt{2x^2+8x+5}-4\sqrt{x}+\sqrt{2x^2-4x+5}-2\sqrt{x}=0\)

\(\Leftrightarrow\dfrac{2x^2+8x+5-16x}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-4x+5-4x}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)

\(\Leftrightarrow\dfrac{2x^2-8x+5}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-8x+5}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)

\(\Leftrightarrow\left(2x^2-8x+5\right)\left(\dfrac{1}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{1}{\sqrt{2x^2-4x+5}+2\sqrt{x}}\right)=0\)

\(\Leftrightarrow2x^2-8x+5=0\)

\(\Leftrightarrow x=\dfrac{4\pm\sqrt{6}}{2}\)

Câu b còn 1 cách giải nữa:

Với \(x=0\) không phải nghiệm

Với \(x>0\) , chia 2 vế cho \(\sqrt{x}\) ta được:

\(\sqrt{2x+8+\dfrac{5}{x}}+\sqrt{2x-4+\dfrac{5}{x}}=6\)

Đặt \(\sqrt{2x-4+\dfrac{5}{x}}=t>0\Leftrightarrow2x+8+\dfrac{5}{x}=t^2+12\)

Phương trình trở thành:

\(\sqrt{t^2+12}+t=6\)

\(\Leftrightarrow\sqrt{t^2+12}=6-t\)

\(\Leftrightarrow\left\{{}\begin{matrix}6-t\ge0\\t^2+12=\left(6-t\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}t\le6\\12t=24\end{matrix}\right.\)

\(\Rightarrow t=2\)

\(\Rightarrow\sqrt{2x-4+\dfrac{5}{x}}=2\)

\(\Leftrightarrow2x-4+\dfrac{5}{x}=4\)

\(\Rightarrow2x^2-8x+5=0\)

\(\Leftrightarrow...\)

\(3\sqrt{8x^2+3}-8x=6\sqrt{2x^2-2x+1}-1\)

\(\Leftrightarrow3\left(\sqrt{8x^2+3}-2\sqrt{2x^2-2x+1}\right)-8x+1=0\)

\(\Leftrightarrow\frac{3\left(8x-1\right)}{\sqrt{8x^2+1}+2\sqrt{2x^2-2x+1}}-\left(8x-1\right)=0\)

\(\Leftrightarrow\left(8x-1\right)\left[\frac{3}{\sqrt{8x^2+3}+2\sqrt{2x^2-2x+1}}-1\right]=0\)

<=> 8x-1=0

<=> x=\(\frac{1}{8}\)

ĐKXĐ: \(x>-\frac{3}{2}\)

\(x+1+\sqrt{2x+3}=\frac{8x^2+18x+11}{2\sqrt{2x+3}}\left(1\right)\)

Đặt \(x+1=a>-\frac{1}{2};\sqrt{2x+3}=b>0\)

\(\Rightarrow8x^2+18x+11=a^2+b^2\)

Khi đó, phương trình (1) trở thành:

\(a+b=\frac{a^2+b^2}{2b}\Leftrightarrow2ab+2b^2=a^2+b^2\)

\(\Leftrightarrow8a^2-2ab-b^2=0\Leftrightarrow\left(2a-b\right)\left(4a+b\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}2a=b\\b=-4a\end{cases}}\)

Với từng trường hợp, bạn thay a,b theo như cách đặt, sau đó bình phương lên và sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn để1 lấy nghiệm và so sánh với điều kiện bài toán nhé!

HỌC TỐT!^_^

Txđ: \(x\in[3;5]\)

Áp dụng BĐT : \(\sqrt{a}+\sqrt{b}\le\sqrt{2\left(a+b\right)}\)Với \(a,b\ge0\)(Chứng minh cái này dễ thôi, bạn bình phương 2 vế là ra nhé)

Ta có: \(\sqrt{5-x}+\sqrt{x-3}\le\sqrt{2(5-x+x-3)}\)\(=2\)

Mặt khác: 

\(\frac{2x^2}{8x-16}=\frac{x^2}{4\left(x-2\right)}=\frac{[\left(x-2\right)+2]^2}{4\left(x-2\right)}=\frac{\left(x-2\right)^2+4\left(x-2\right)+4}{4\left(x-2\right)}=\frac{x-2}{4}+\frac{1}{x-2}+1\)

\(\ge2\sqrt{\frac{x-2}{4}.\frac{1}{x-2}}+1=2\)

Dấu "=" xảy ra khi: \(\hept{\begin{cases}5-x=x-3\\\frac{x-2}{4}=\frac{1}{x-2}\end{cases}}\)

=> \(x=4\)(Thỏa mãn Đ/K)