Cho hình bình hành ABCD, gọi E,f theo thứ tự là trung điểm của AB,CD ,gọi M là giao điểm của AF và DE , N là gđ của BF và CE .Chứng minh 3 đường thẳng AC,EF,MN đồng quy
Cho hình hình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng: Các đường thẳng AC, EF, MN đồng quy.
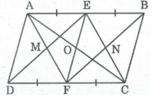
Gọi O là giao điểm của AC và EF
Tứ giác AECF là hình bình hành ⇒ OE = OF
Tứ giác EMFN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Suy ra: MN đi qua trung điểm O của EF.
Vậy AC, EF, MN đồng quy tại O.
Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE. N là giao điểm của BF và CE. Chứng minh rằng :
a) EMFN là hình bình hành
b) Các đường thẳng AC, EF, MN đồng quy
cho hình bình hành ABCD gọi E,F theo thứ tự là trung điểm của AB,CD Gọi M là giao điểm của AF và DE, N là giao điểm BF và CE
a) CMR EMFN là hình bình hành
b) Các Đường thẳng AC, EF, MN Đồng quy
Cho hình bình hành ABCD. Gọi E, F là trung điểm AB,CD. Gọi M là giao điểm của AF và DE, N là giao điểm BF và CE. Chứng minh:
a) EMFN là hình bình hành
b) Các đường thẳng AC, EF, MN đồng quy
làm đc mỗi câu b :))
AEFC là hình bình hành ( tự cm nhá :) )
=> đường chéo AC giao đường chéo EF tại trung điểm của EF
câu a => đường chéo MN giao đường chéo EF tại trung điểm của EF
=> ĐPCM
câu b thui, câu a lằng nhằng quá lười nghĩ thông cảm nhé
Cho hình bình hành ABCD. Gọi E, F là trung điểm AB,CD. Gọi M là giao điểm của AF và DE, N là giao điểm BF và CE. Chứng minh:
a) EMFN là hình bình hành
b) Các đường thẳng AC, EF, MN đồng quy
Cho hình bình hành ABCD. Gọi E, F là trung điểm AB,CD. Gọi M là giao điểm của AF và DE, N là giao điểm BF và CE. Chứng minh:
a) EMFN là hình bình hành
b) Các đường thẳng AC, EF, MN đồng quy
Cho ABCD là hình bình hành. Gọi E và F theo thứ tự là trung điểm của AB và CD. Gọi M là giao điểm của AF và CE. Gọi M là giao điểm của BF và CE. Chứng minh rằng
a) EMFN là hình bình hành
b) AC và EF và MN đồng quy
a, Ta có: ABCD la hình bình hành
=> AB=CD; AB//CD
Mà E là trung điểm của AB; F là trung điểm của CD.
=>AE= EB= CF= DF (1)
VÌ AB// CD=>EB// DF (2)
Từ(1) và (2) => EBFD là hình bình hành (theo dấu hiệu nhận biết hình bình hành)(đpcm)
b, Xét hbh ABCD ta có:
AC cắt BD tại trung điểm của AC và BD (1)
Xét hình bình hành EBFD có EF cắt BD tại trung điểm của EF và BD (2)
Từ (1) và (2) => Ba đường thẳng AC, BD, EF đồng quy
Cho Hình bình hành ABCD . Gọi E,F theo thứ tự là trung điển của AB,CD
Gọi M là giao điểm của F và DE ,N là giao điển của BF và CE
a) C/m : EMFN là hình bình hành
b)c/m các đường thẳng AC , EF , MN đồng quy
Chi hình bình hành ABCD . Gọi E,F theo thứ tự là trung điểm của AB,CD. Gọi M là giao điểm của À và DE, N là giao điểm của BF và CE.Chứng minh rằng:
a, EMFN là hình bình hành
b, Các đường thẳng AC,EF,MN đồng quy
làm đc mỗi câu b :))
AEFC là hình bình hành ( tự cm nhá :) )
=> đường chéo AC giao đường chéo EF tại trung điểm của EF
câu a => đường chéo MN giao đường chéo EF tại trung điểm của EF
=> ĐPCM