cho hình vẽ biết PA//PB, SA//SB, QA//QB. chứng minh P, Q, S THẲNG HÀNG

Những câu hỏi liên quan
Cho tam giác ABP có PA=PB;S là 1 điểm nằm trong tâm tam giác APB SAO CHO SA = SB.Q là 1 điểm nằm trên nửa mặt phẳng có bờ là tia AB không chứa S và P sao cho QA=QB
CMP.3 điểm P,Q,S THẲNG HÀNG
Cho tam giác ABP có PA=PB;S là 1 điểm nằm trong tâm tam giác APB SAO CHO SA = SB.Q là 1 điểm nằm trên nửa mặt phẳng có bờ là tia AB không chứa S và P sao cho QA=QB
CMP.3 điểm P,Q,S THẲNG HÀNG
Cho a,b,c,p,q là 5 số dương tùy ý . Chứng minh
\(\frac{a}{pb+qc}+\frac{b}{pc+qa}+\frac{c}{pa+qb}\ge\frac{3}{p+q}\)
Ai nhanh tick
\(A=\frac{a}{pb+qc}+\frac{b}{pc+qa}+\frac{c}{pa+qb}\)
\(\Rightarrow A=\frac{a^2}{pab+qac}+\frac{b^2}{pbc+qab}+\frac{c^2}{pac+qbc}\)
\(\Rightarrow A\ge\frac{\left(a+b+c\right)^2}{p\left(ab+bc+ca\right)+q\left(ab+bc+ca\right)}\)
\(\Rightarrow A\ge\frac{3\left(ab+bc+ca\right)}{\left(p+q\right)\left(ab+bc+ca\right)}=\frac{3}{p+q}\)
Đúng 0
Bình luận (0)
Ta đặt kí hiệu bất đẳng thức cần chứng minh là (1)
Ta thấy : \(a=\sqrt{\frac{a}{pb+qc}}\cdot\sqrt{a\left(pb+qc\right)}\)
\(b=\sqrt{\frac{b}{pc+qa}}\cdot\sqrt{b\left(pc+qa\right)}\)
\(c=\sqrt{\frac{c}{pa+qb}}\cdot\sqrt{c\left(pa+qb\right)}\)
Gọi vế trái của bất đẳng thức (1) là H
Ta có : \(\left(a+b+c\right)^2=\)(\(\sqrt{\frac{a}{pb+qc}}\cdot\sqrt{a\left(pb+qc\right)}\)+ \(\sqrt{\frac{b}{pc+qa}}\cdot\sqrt{b\left(pc+qa\right)}\)+ \(\sqrt{\frac{c}{pa+qb}}\cdot\sqrt{c\left(pa+qb\right)}\))2 \(\le\)\(\text{H}.\left[a\left(pb+qc\right)+b\left(pc+qa\right)+c\left(pa+qb\right)\right]\)
= \(\text{H}\left(p+q\right)\left(ab+bc+ca\right)\) (2)
Mặt khác : \(ab+bc+ca\le\frac{1}{3}\left(a+b+c\right)^2\)
bới : \(3\left(ab+bc+ca\right)=\left(ab+bc+ca\right)+2\left(ab+bc+ca\right)\)\(\le\)\(a^2+b^2+c^2+2\left(ab+bc+ca\right)=\left(a+b+c\right)^2\)
Với kq trên từ (2) ta suy ra được : \(\left(a+b+c\right)^2\le\text{H}\left(p+q\right)\cdot\frac{\left(a+b+c\right)^2}{3}\)
\(\Rightarrow\text{H}\ge\frac{3}{p+q}\left(\text{vì }a+b+c>0,p+q>0\right)\)
Vậy \(\frac{a}{pb+qc}+\frac{b}{pc+qa}+\frac{c}{pa+qb}\ge\frac{3}{p+q}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
1. Cho a, b, c, d, p, q là 5 số dương tùy ý . Chứng minh
\(\frac{a}{pb+qc}+\frac{b}{pc+qa}+\frac{c}{pa+qb}\ge\frac{3}{p+q}\)
2. Cho a, b, c là ba số dương cho trước, còn x, y, z là ba số dương thay đổi, luôn luôn thỏa mãn điều kiện :
\(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=1\)
Tìm GTLN của tổng S = x + y + z
dcv_new
\(\Sigma\frac{a^2}{pab+qca}\ge\frac{\left(a+b+c\right)^2}{\left(p+q\right)\left(ab+bc+ca\right)}\ge\frac{3}{p+q}\)
2, ta có \(\sqrt{a}=\sqrt{\frac{a}{x}}\cdot\sqrt{x}\)
vậy ta được \(\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2=\left(\sqrt{\frac{a}{x}}\cdot\sqrt{x}+\sqrt{\frac{b}{y}}\cdot\sqrt{y}+\sqrt{\frac{c}{z}}\cdot\sqrt{z}\right)^2\le\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right)\left(x+y+z\right)=S\)
dấu đẳng thức xảy ra khi \(\sqrt{x}:\sqrt{\frac{a}{x}}=\sqrt{y}:\sqrt{\frac{b}{y}}=\sqrt{z}:\sqrt{\frac{c}{z}}\Leftrightarrow\hept{\begin{cases}\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=1\\\frac{x}{\sqrt{a}}=\frac{y}{\sqrt{b}}=\frac{z}{\sqrt{c}}\end{cases}}\)
\(\Rightarrow x=\frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}};y=\frac{\sqrt{b}}{\sqrt{a}+\sqrt{b}+\sqrt{c}};z=\frac{\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
vậy min (x+y+z)=\(\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2\)
À nhầm đề 1 tí . Sửa thành a, b, c , p , q
Đánh máy nhanh quá nên nhầm xíu =)
Xem thêm câu trả lời
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâmO. Gọi M, N, P, Q lần lượt là trung điểm của BC, SB, SA, OP. a) Chứng minh mặt phẳng (OMN) song song với mặt phẳng (SCD). (0,5 điểm +vẽ hình 0,5 điểm) b) Chứng minh đường thẳng MQ song song với mặt phẳng (SCD). (0,5 điểm)Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâmO. Gọi I là điểm thuộc AO, (P) là mặt phẳng đi qua I và song songvới mặt phẳng (SBD). Xác định thiết diện của hình chóp cắt bởi mặtphẳng (P). ( 1,0 điể...
Đọc tiếp
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm
O. Gọi M, N, P, Q lần lượt là trung điểm của BC, SB, SA, OP.
a) Chứng minh mặt phẳng (OMN) song song với mặt phẳng
(SCD). (0,5 điểm +vẽ hình 0,5 điểm)
b) Chứng minh đường thẳng MQ song song với mặt phẳng
(SCD). (0,5 điểm)
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm
O. Gọi I là điểm thuộc AO, (P) là mặt phẳng đi qua I và song song
với mặt phẳng (SBD). Xác định thiết diện của hình chóp cắt bởi mặt
phẳng (P). ( 1,0 điểm)
Cho tam giác ABC.Điểm P\(\in\)tia AC,Q\(\in\)tia CB.Đường thẳng PQ cắt đường thẳng AB tại R.Các đường thẳng AQ và BP cắt nhau tại I.Đường thẳng CI cắt AB tại S
a)CMR \(\frac{RA}{RB}.\frac{QB}{QC}.\frac{PC}{PA}=1\)
b\(\frac{SA}{SB}=\frac{RA}{RB}\)
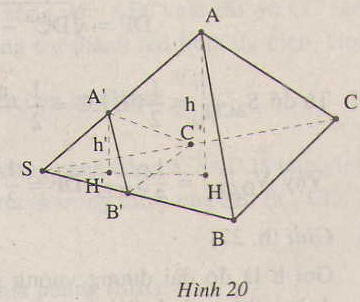
Cho hình chóp S.ABC. Trên các đoạn thẳng SABC. Trên các đoạn thẳng SA, SB, SC lần lượt lấy ba điểm A', B', C' khác với S. Chứng minh rằng :
\(\dfrac{V_{S.A'B'C'}}{V_{S.ABC}}=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}\)
Gọi h và h’ lần lượt là chiều cao hạ từ A, A’ đến mặt phẳng (SBC).
Gọi S1 và S2 theo thứ tự là diện tích các tam giác SBC và SB’C’.
Khi đó ta có h′h=SA′SAh′h=SA′SA và 12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC
Suy ra VS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SCVS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SC
Đó là điều phải chứng minh.
Đúng 0
Bình luận (0)
Từ điểm S nằm ngoài đường tròn tâm (O;R) vẽ hai tiếp tuyến SA;SB (A;B là các tiếp điểm ). Cát tuyến SMN cắt bán kính OB. Gọi Q là trung điểm MN .a)Chứng minh tứ giác SAOQ nội tiếp đường tròn .b)Chứng minh QS là phân giác của góc AQB . c)Qua Q vẽ đường thẳng vuông góc với OS cắt tia SA,SB thứ tự tại C,D. Khi (O;R) và đường thẳng MN cố định .Tìm vị trí của S trên đường thẳng MN để diện tích tam giác SCD nhỏ nhất
Đọc tiếp
Từ điểm S nằm ngoài đường tròn tâm (O;R) vẽ hai tiếp tuyến SA;SB (A;B là các tiếp điểm ). Cát tuyến SMN cắt bán kính OB. Gọi Q là trung điểm MN .
a)Chứng minh tứ giác SAOQ nội tiếp đường tròn .
b)Chứng minh QS là phân giác của góc AQB .
c)Qua Q vẽ đường thẳng vuông góc với OS cắt tia SA,SB thứ tự tại C,D. Khi (O;R) và đường thẳng MN cố định .Tìm vị trí của S trên đường thẳng MN để diện tích tam giác SCD nhỏ nhất
Cho hình vuông ABCD, O là giao điểm hai đường chéo AC và BD . Trên đường thẳng vuông góc với mp(ABCD) tại B, lấy điểm S và nối S với A,B,C,D a)Chứng minh mp(SAC) vuông góc mp(SBD)
b) gọi m,n,p,q lần lượt là trung điểm của sa ,sb,sc,sd .chứng minh mp(mnpq)//mp(abcd)
c)tứ giác mnpq là hình gì? tính diện tích của tứ giác khi biết ab=a
Cho tứ diện S.ABC có D, E lần lượt trung điểm AC, BC và G là trọng tâm tam giác ABC. Mặt phẳng (α) qua AC cắt SE, SB lần lượt tại M, N. Một mặt phẳng (β) qua BC cắt SD và SA lần lượt tại P và Q.
a) Gọi I = AM ∩ DN, J = BP ∩ EQ. Chứng minh bốn điểm S, I, J, G thẳng hàng.
b) Giả sử AN ∩ DM = K, BQ ∩ EP = L. Chứng minh ba điểm S, K, L thẳng hàng.
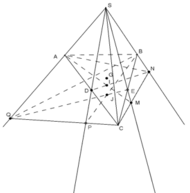
a) Ta thấy:
+ G là trọng tâm tam giác ABC ⇒ G ∈ BD ⇒ G ∈ BD
+ I ∈ DN (theo cách dựng hình).
+ J ∈ BP (theo cách dựng hình).
⇒ S, I, J, G ∈ mp(SPN)
Tương tự ⇒ S, I, J, G ∈ mp(SQM)
Vậy S, I, J, G là điểm chung của mp(SPN) và mp(SQM)
b)
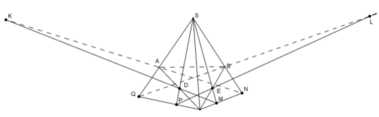
Ta thấy:
+ S = PD ∩ EM
+ K ∈ DM
+ L ∈ PE
⇒ S, K, L ∈ (SPM)
Tương tự ⇒ S, K, L ∈ (SQN)
Vậy S, K, L là điểm chung của (SPM) và (SQN)
Đúng 0
Bình luận (0)


















