Vẽ lần lượt đoạn thẳng AB, tia AB, đường thẳng AB trên cùng một hình

Những câu hỏi liên quan
Vẽ lần lượt đoạn thẳng AB , tia AB , đường thẳng AB trên cùng một hình
30 , Vẽ lần lượt đoạn thẳng AB , tia AB , đường thẳng AB trên cùng một hình
Vẽ lần lượt đoạn AB, tia AB, đường thẳng AB trên cùng một hình:
Vẽ lần lượt đoạn thẳng AB, tia AB, đường thẳng AB trên cùng một hình
Xem thêm câu trả lời
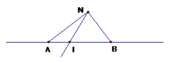
a) Vẽ lần lượt đoạn thẳng AB, tia AB, đường thẳng AB trên cùng một hình;
b) Lấy điểm I thuộc đoạn thẳng AB (I khác A và B) và điểm N không thuộc đường thẳng AB;
c) Vẽ các đoạn thẳng NA, NB và tia NI.
Vẽ lần lượt đoạn thẳng AB, tia AB, đường thẳng AB trên cùng một hình
giúp mình với mn ơi
cho đoạn thẳng ab trên cùng một nửa mặt phẳng ab vẽ hai tia ã, by cùng vuông góc với ab gọi o là trung điểm ab trên tia ã by lần lượt lấy hai điểm C và D bất kỳ sao cho COD = 90 chứng minh Cd là tiếp tuyến của hai đường tròn đường kính AB tìm vị trí của C D để diện tích tứ giác ABDC nhỏ nhất và tính diện tích ấy theo AB = a
Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ hai tia Ax và By lần lượt vuông góc với AB tại A và B. Gọi O là trung điểm của đoạn thẳng AB. Trên tia Ax lấy điểm C và trên tia By lấy điểm D sao cho góc COD=90 độ.
a) Chúng minh rằng AC+BD=CD
b) Chứng minh rằng AC.BC=AB^2/4
Bạn tự vẽ hình nha
Câu a
Chứng minh : Kẻ OC cắt BD tại E
Xét ΔCAO và ΔEBO có :
ˆA=^OBE (=1v)
AO=BO (gt)
^COA=^BOE (đối đỉnh)
⇒ΔCAO=ΔEBO (cgv - gn )
⇒OC=OE ( hai cạnh tương ứng )
và AC=BE ( hai cạnh tương ứng )
Xét ΔOCD và ΔOED có :
OC=OE (c/m trên )
^COD=^DOE ( = 1v )
OD chung
⇒ΔOCD=ΔOED (cgv - cgv )
⇒CD=DE (hai cạnh tương ứng )
mà DE = BD + BE
và AC = BE ( c/m trên )
⇒CD=AC+BD
Đúng 0
Bình luận (0)
bạn có đọc nội quy không bạn Nguyễn Minh Huy, k k linh tinh nhé, (dcmm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ tia Ax và By sao cho BAx 120 độ, ABy60 độ. Trên tia Bylấy điểm C và trên tia đối của tia Ax lấy điểm D sao cho AD BC. Gọi O là giao điểm của AB và CD.a. Chứng minh O là trung điểm của mỗi đoạn thẳng AB, CD.b. Qua O vẽ một đường thẳng cắt đường thẳng AD và BC lần lượt ở E và F. Chứng minh O là trung điểm của EF.c. Gọi M, N lần lượt là trung điểm của AD, BC. Chứng minh O là trung điểm của MN.
Đọc tiếp
Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ tia Ax và By sao cho BAx = 120 độ, ABy=60 độ. Trên tia By
lấy điểm C và trên tia đối của tia Ax lấy điểm D sao cho AD = BC. Gọi O là giao điểm của AB và CD.
a. Chứng minh O là trung điểm của mỗi đoạn thẳng AB, CD.
b. Qua O vẽ một đường thẳng cắt đường thẳng AD và BC lần lượt ở E và F. Chứng minh O là trung điểm của EF.
c. Gọi M, N lần lượt là trung điểm của AD, BC. Chứng minh O là trung điểm của MN.