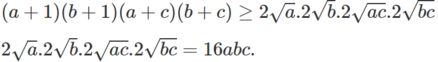Với ba tập hợp A,B,C tùy ý chứng minh: (A\B)\C = (A\B)\(A\C)
Những câu hỏi liên quan
Cho A,B,C là các tập tùy ý. Chứng minh rằng A trừ (B trừ C) bằng (A trừ B ) hợp ( A giao C)
30 tháng 9 2021 lúc 16:21
Bài 1: Cho các tập hợp: A{1;2;3}, B{2;3;6;7}, C{3;4;5;8}a)Tìm AcapB, AcupB, AB, BAb)Chứng minh Acap(BC)(AcapB)AcapC)Bài 2: Cho A là một tập hợp tùy ý. Xác định các tập hợp sau:a)AcapA; AcupA; Acapvarnothing; Acupvarnothingb)AA; Avarnothing; varnothingA
Đọc tiếp
Bài 1: Cho các tập hợp: A={1;2;3}, B={2;3;6;7}, C={3;4;5;8}
a)Tìm A\(\cap\)B, A\(\cup\)B, A\B, B\A
b)Chứng minh A\(\cap\)(B\C)=(A\(\cap\)B)\(A\(\cap\)C)
Bài 2: Cho A là một tập hợp tùy ý. Xác định các tập hợp sau:
a)A\(\cap\)A; A\(\cup\)A; A\(\cap\)\(\varnothing\); A\(\cup\)\(\varnothing\)
b)A\A; A\\(\varnothing\); \(\varnothing\)\A
Chứng minh rằng:
(a + 1)(b + 1)(a + c)(b + c) ≥ 16abc, với a, b, c là những số dương tùy ý.
Chứng minh rằng với mọi bộ ba số khác 0 tùy ý \(a,b,c\) luôn có \(\frac{a^2}{b^2}+\frac{b^2}{c^2}+\frac{c^2}{a^2}\ge\frac{c}{b}+\frac{b}{a}+\frac{a}{c}\).
Cho tam giác $A B C$ và một điểm $M$ tùy ý. Gọi $A^{\prime}, B^{\prime}, C^{\prime}$ lân lượt là các điêm đôi xứng của $M$ qua các trung điểm $K, I, J$ của các cạnh $B C, C A, A B$.
a) Chứng minh ba đường thẳng $A A^{\prime}, B B^{\prime}, C C^{\prime}$ đồng quy tại một điểm $N$.
b) Chứng minh rằng khi $M$ di động thì đường thẳng $M N$ luôn đi qua trọng tâm $G$ của $\triangle A B C$.
Chứng minh rằng: a^2 + b^2 + c^2 > hoặc = ab + ac + bc với a; b; c tùy ý
Giả sử:
2a^2 + 2b^2 + 2c^2 > hoặc = 2ab + 2ac + 2bc
<=>( a^2 -2ab + b^2) + (a^2 -2ac + c^2)+(b^2 -2bc + c^2) > hoặc = 0
=<=>(a-b)^2 + (a-c)^2 + (b-c)^2 > hoặc = 0 ( BĐT luôn đúng ) => 2a^2 + 2b^2 + 2c^2 >hoặc = 2ab + 2ac + 2bc là đúng ! <=> a^2 + b^2 + c^2 > hoặc = ab+bc+ac.
Dấu = xảy ra khi : a=b=c
Đúng 0
Bình luận (0)
Trong không gian cho ba vecto tùy ý
a
→
,
b
→
,
c
→
Gọi
u
→
a
→
− 2
b
→
,
v
→
3
b
→
−
c...
Đọc tiếp
Trong không gian cho ba vecto tùy ý a → , b → , c →
Gọi u → = a → − 2 b → , v → = 3 b → − c → , w → = 2 c → − 3 a →
Chứng tỏ rằng ba vecto u → , v → , w → đồng phẳng.
Muốn chứng tỏ rằng ba vecto u → , v → , w → đồng phẳng ta cần tìm hai số thực p và q sao cho w → = p u → + q v →
Giả sử có w → = p u → + q v →
2 c → – 3 a → = p( a → – 2 b → ) + q(3 b → − c → )
⇔ (3 + p) a → + (3q − 2p) b → − (q + 2) c → = 0 → (1)
Vì ba vecto lấy tùy ý a → , b → , c → nên đẳng thức (1) xảy ra khi và chỉ khi:
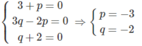
Như vậy ta có: w → = −3 u → − 2 v → nên ba vecto u → , v → , w → đồng phẳng.
Đúng 0
Bình luận (0)
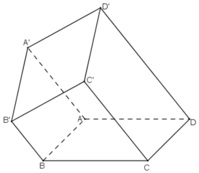
Trong mặt phẳng (α) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d song song với nhau và không nằm trên (α). Trên a, b và c lần lượt lấy ba điểm A’, B’ và C’ tùy ý.
a) Hãy xác định giao điểm D’ của đường thẳng d với mặt phẳng (A’B’C’).
b) Chứng minh A’B’C’D’ là hình bình hành.
a) Giả sử (A’B’C’) ∩ d = D’
⇒ (A’B’C’) ∩ (C’CD) = C’D’.
+ AA’ // CC’ ⊂ (C’CD)
⇒ AA’ // (C’CD).
AB // CD ⊂ (CC’D)
⇒ AB // (CC’D)
(AA’B’B) có:
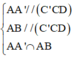⇒ (AA’B’B) // (C’CD).
Mà (A’B’C’) ∩ (AA’B’B) = A’B’
⇒ (A’B’C’) cắt (C’CD) và giao tuyến song song với A’B’
⇒ C’D’ // A’B’.
b) Chứng minh tương tự phần a ta có B’C’ // A’D’.
Tứ giác A’B’C’D’ có: B’C’ // A’D’ và C’D’ // A’B’
⇒ A’B’C’D’ là hình bình hành.
Đúng 0
Bình luận (0)
Chứng minh rằng với a, b, c, d tùy ý ta luôn có:
\(a^2+b^2+c^2+d^2\ge\left(a+b\right)\left(c+d\right)\)
dễ lăm chỉ cần áp dụng bài toán phụ a2+b2>=2ab là ra chúc bạn làm được bài tốt nhé mình chỉ gợi ý cho thôi
Đúng 0
Bình luận (0)
vũ tiền châu: Bạn có thể nói rõ hơn một chút được không ạ? Vậy có cần biến đổi c^2+ d^2>=2cd không?
Đúng 0
Bình luận (0)
Xem thêm câu trả lời